(Letzte Änderung: 19.April 2023, 07:00h)
KONTEXT
Dieser Text ist Teil des Lehrprojektes ‚Citizen Science für Nachhaltige Entwicklung‘ im Sommersemester 2023.
ZUSAMMENFASSUNG
Nach einer kurzen Erklärung des Kontextes ‚Lehrprojekt‘ wird nochmals an die Konzepte ‚empirische Theorie‘ und ’nachhaltige empirische Theorie‘ erinnert. Dann wird auf die konkrete Gemeinde verwiesen, die als Beispiel-Kommune dienen soll. Dann wird das Konzept (nachhaltige) empirische Theorie mit ihren drei Komponenten (i) akzeptierte Ausgangslage, (ii) akzeptierte ‚Veränderungsregeln, und (iii) Vereinbarung (oft ‚Folgerungsbegriff‘ genannt) beispielhaft erläutert. Es folgt dann ein konkretes Beispiel, das mit Hilfe eines ‚Rechenblatts‘ illustriert wird. Abschließend erfolgt dann auf der Basis des vorausgehenden Beispiels eine Erläuterung zum Konzept ‚Bewertung‘, wodurch aus einer empirischen Theorie eine ’nachhaltige empirische Theorie‘ werden kann.
BEVÖLKERUNGSENTWICKLUNG
Im Rahmen des Lehrprojektes wurden per Zufall 6 Teams gebildet (unter Berücksichtigung einer guten Verteilung nach Fachbereichen). Zusätzlich gibt es ein Querschnittsthema:
- Wald
- Wasser
- Energie-Versorgung
- Finanzen der Gemeinde
- Landwirtschaft & Ernährung
- Verkehr
- QUERSCHNITT: Bevölkerung
Diese Themen (außer dem Querschnitts-Thema) wurden den sechs Teams zugelost. Es ist Aufgabe jeden Teams, das Thema zu analysieren und es im Format eines ‚Spiels‘ aufzubereiten, wobei ‚Spiel‘ hier gesehen wird als eine Form von ‚Nachhaltiger Empirischer Theorie‘.
In diesem Text wird nur das Thema ‚Bevölkerungsentwicklung‘ durchgespielt: Wie kann man das Thema im Format eines Spiels mit möglichst großem Empiriebezug entwickeln?
In diesem Text wird das ‚Konzept‘ vorgestellt, was es heißt, ein Thema als ‚Spiel‘ zu formatieren, das den Anforderungen einer ’nachhaltigen empirischen Theorie‘ genügt. In einem weiteren Text (geplant für 3.Mai 2023) soll dann eine ‚Umsetzung‘ (‚Implementierung‘) in eine neue Software speziell für das Editieren und Simulieren von nachhaltigen empirischen Theorien gezeigt werden. Die studentischen Teams sind aber völlig frei, welche Formatierung sie selbst wählen. Es gibt unendlich viele Möglichkeiten. Aus jeder kann man etwas lernen.
Nachhaltige Empirische Theorie
Wie schon im Beitrag ‚Grundbegriffe‘ [1] kurz beschrieben wird, repräsentiert eine ‚Nachhaltige Empirische Theorie (NET)‘ eine Kombination aus ‚Empirischer Theorie (ET)‘ und einer Menge von ‚minimalen Präferenzen‘ (‚Werten‘) im Format ‚A ist besser als B‘ bzw. ‚B ist weniger Wert als A‘.
Die empirische Theorie beschreibt nur, welche wahrscheinlichen Folgen eintreten werden, wenn eine bestimmte Situation aktuell gegeben ist. Eine empirische Theorie selbst bewertet nicht.
Im Alltagsleben reicht ein bloßes Wissen darum, was eintreten kann, aber nicht aus (so wertvoll auch diese Erkenntnis als solche sein mag). Als Menschen müssen wir meistens handeln und im Handeln entscheiden wir faktisch, was in der nahen — und fernen — Zukunft möglicherweise ‚der Fall sein wird‘.
Empirisches Wissen, das aus Experimenten entsteht, und Präferenz-Wissen, das auf der Basis von Erfahrungen durch ’subjektive Entscheidungen der Akteure‘ entsteht, kann im Alltagshandeln in Kombination eine große Hilfe sein: mit dem empirischen Wissen kann man wissen, was generell möglich ist, und mit einem Präferenzwissen kann man ‚bewusst auswählen‘, welche der bekannten Möglichkeiten man ‚auswählen sollte‘.
Normalerweise ist es nicht die Absicht der ‚Handelnden‘, eine Situation ‚bewusst zu verschlechtern‘. Im Gegenteil, im ‚Lichte des verfügbaren Wissens‘ versucht man eher nur jene Handlungen vorzunehmen, die nicht bewusst schädigen, eher das Gegenteil. Dies ist aber nur möglich, wenn die Handelnden über ein explizites Wissen um ‚Präferenzen‘ verfügen. Wie bekannt, können Präferenzen allerdings auch ‚falsch‘ sein, obgleich die Handelnden glauben, dass sie das ‚Richtige‘ tun.
Im Rahmen eines ‚echten Lernens‘ sind ‚Irrtümer‘ immer möglich; sie helfen, ‚falsche Optionen‘ zu erkennen und können das System der Präferenzen optimieren.
Beispiel Bevölkerungsentwicklung
Angewendet auf das Thema ‚Bevölkerungsentwicklung‘ bedeutet dies, man benötigt in einem ersten Schritt (i) eine ‚empirische Theorie‘, wie sich eine Bevölkerung entwickeln kann, und in einem zweiten Schritt (ii) Präferenzen, welche möglichen Entwicklungen ‚eher wünschenswert‘ sind und welche ‚eher nicht wünschenswert‘ sind.
Dies sollte jeweils auf das Beispiel 61137 Schöneck angewendet werden.
Darüberhinaus wäre es hilfreich, wenn man die Bevölkerungsentwicklung in der Kommune Schöneck nicht isoliert, sondern im Zusammenhang mit der Umgebung betrachtet. Als nächstes bietet sich der zugehörige ‚Landkreis‘ an; dies ist der Main-Kinzig Kreis (MKK). Darüber hinaus könnte man auch noch zum Regierungsbezirk Darmstadt schauen, zum Land Hessen, auf Deutschland, auf Europa und letztlich auf die gesamte Weltbevölkerung. In diesem Text wird zunächst nur die Kommune Schöneck betrachtet und ansatzweise der Main-Kinzig Kreis.
Konkretisierung einer Empirischen Theorie
Zunächst sollen die Anforderungen geklärt werden, die notwendig sind, um eine einfache empirische Theorie (ET) für die Problemstellung ‚Bevölkerungsentwicklung‘ entwickelt zu können.
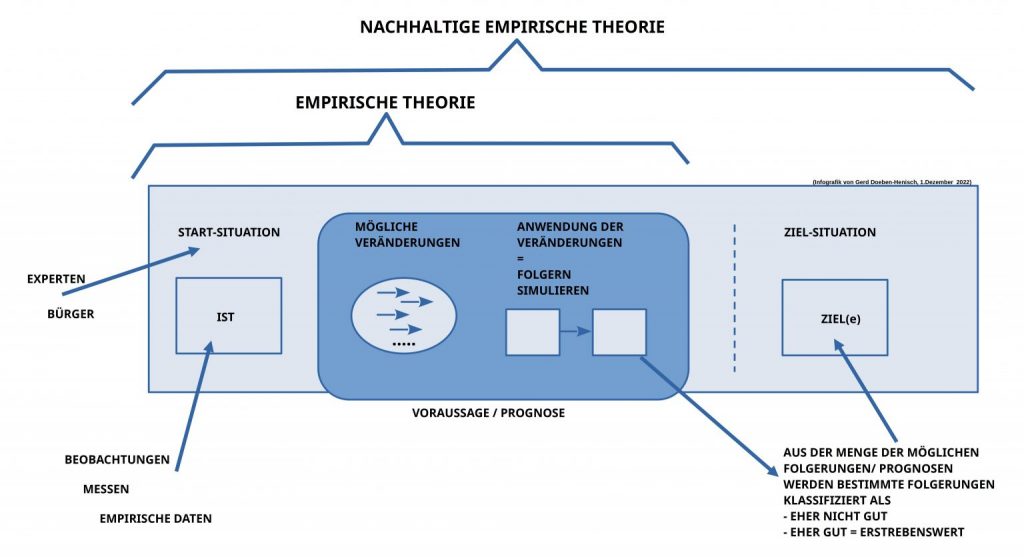
Wie das vorausgehende Schaubild nochmals erinnert, benötigt eine ‚empirische Theorie (ET)‘ mindestens drei Elemente: (i) die Beschreibung einer allgemein akzeptierten Ausgangslage, (ii) eine Menge von akzeptierten ‚Veränderungsregeln, und (iii) eine Vereinbarung (oft ‚Folgerungsbegriff‘ genannt), wie man Veränderungsregeln auf eine gegebene Situation anwenden kann.
Ausgangslage für Bevölkerungsentwicklung
Es stellt sich dann die Frage, wie soll das Konzept ‚Ausgangslage‘ im Fall der angedachten Theorie der Bevölkerungsentwicklung am Beispiel der Gemeinde Schöneck (bzw. dann auch des MKK) beschaffen sein?
Ausgangspunkt ist eine Gruppe von ‚Bürgern‘, die solch eine Ausgangslage erstellen wollen.
Generell soll die ‚Beschreibung einer Ausgangslage‘ ein ‚Text‘ sein. Zusätzlich wird angenommen, dass dieser Text in ‚Alltagssprache‘ (hier: Deutsch) abgefasst sein soll.
Angenommen, die beteiligten Bürger haben verschiedene Wissensvoraussetzungen (was der Normalfall wäre), dann müssen diese sich zunächst mal darauf einigen, was denn alles für solch eine Beschreibung gebraucht wird.
Es folgt eine erste ungeordnete Liste von Annahmen, die als Ergebnis einer ersten (fiktiven) Diskussionsrunde der Gruppe der Bürger verstanden werden soll.
- Als Raumgebiet wird das Gebiet der Gemeinde Schöneck angenommen.
- Als ‚Bevölkerung‘ solle die Menge der ‚Einwohner‘ zählen, also jene Menschen, die in der Gemeinde Schöneck zu einem bestimmen ‚Stichtag‘ gemeldet sind.
Es ist dann zu klären, welche zusätzlichen Eigenschaften der Einwohner erfasst werden müssten, um eine notwendige Versorgung der Bürger seitens der Gemeinde sicher stellen zu können, wie z.B.:
- Kindergarten
- Schulen
- ÖPNV
- Gesundheitsdienste
- Einkaufen
- Müll
- Wasser
- Energie
- ….
Mögliche Veränderungen
Da die Welt, in der wir uns befinden sich überwiegend in ständiger Veränderung befindet, ist es wichtig zu klären, in welcher Weise sich die Bevölkerung einer Kommune verändern kann. Folgende minimale Annahmen werden (versuchsweise) getroffen:
- Geburten
- Sterbefälle
- Neuanmeldung
- Abmeldungen
Wie wir wissen, können diese Formen von Veränderungen von konkreten Voraussetzungen abhängen, diese dann wieder von anderen Voraussetzungen, usw. Begonnen werden soll hier mit den ersten beiden Formen von Veränderungen: Geburten und Sterbefälle.
Regel-Anwendung
Eine Regel nützt nur dann etwas, wenn man auch weiß, wann man die Regel wie auf eine gegebene Situation anwenden kann. Die Regel-Anwendung wird in der Theorie mit einem ‚Folgerungsbegriff‘ definiert, und in einem Spiel mit einer ‚Spielanleitung‘.
Eine Anwendungs-Regel könnte ungefähr lauten: Wenn ich in einem Jahr N-viele Einwohner habe und der Zuwachs pro Jahr beträgt z=0.15 (15%), dann beträgt die Zahl der Einwohner im Folgejahr N+1 = N+(N*z):
| EINWOHNER | ZUNAHME pro JAHR | EINWOHNER IM FOLGEJAHR |
| N | z | N+1 |
| N+1=N+(N*z) | ||
| 1000 | 0,15 | 1150 |
Eine Regel-Anwendung könnte dann darin bestehen, dass man erklärt, wie man die Veränderung ‚Zuwachs‘ z=0,15 auf die gegebene Einwohnerzahl N=1000 anwendet, z.B. N+1=N+(N*z). Entsprechend dann mit einer Abnahme s=0,16:
| EINWOHNER | ABNAHME pro JAHR | EINWOHNER IM FOLGEJAHR |
| s | ||
| N+1 = N – (N*s) | ||
| 1000 | 0,16 | 840 |
| EINWOHNER | ZUNAHME + ABNAHME | EINWOHNER IM FOLGEJAHR |
| z=0,15 | ||
| s=0,16 | ||
| 1000 | N1 = N+(N*z)– (N*s) | |
| 990 |
In der Kombination von ‚Zuwachs‘ und ‚Abnahme‘ müsste man zwei Operationen auf die Ausgangslage N anwenden, etwa: N1 = N+(N*z)– (N*s). Man würde im Folgejahr ‚990‘ erhalten, was einer Verminderung der Einwohnerzahl gleichkommt. Würde sich diese Verminderung in den weiteren Jahren fortsetzen, dann hätte dies verheerende Folgen für die Existenz des Ortes.
Theorie im Spielformat
Die bisherigen drei Aufgaben
(i) akzeptierte Ausgangslage, (ii) akzeptierte ‚Veränderungsregeln, und (iii) Vereinbarung (oft ‚Folgerungsbegriff‘ genannt), wie man Veränderungsregeln auf eine gegebene Situation anwenden kann.
kann man nun entweder im Stil einer formalisierten ‚Theorie‘ weiter ausformulieren oder eben im Stil eines ‚Spiels‘. Letzteres soll hier exemplarisch — noch auf ‚konzeptioneller Ebene‘ — geschehen.
Ausgangslage Bevölkerung
Im bisherigen Beispiel bietet es sich an, von folgenden minimalen Annahmen auszugehen:
- Es gibt eine EINWOHNERZAHL (E)
- Es gibt einen Kalender, der im Fall der Einwohner nur Jahreszahlen enthält, also immer ein bestimmtes JAHR (T), für das die Einwohnerzahl festgestellt wurde.
- Es gibt ein ‚RAUMGEBIET‘, das sich einer ‚offiziellen KARTE‘ zuordnen lässt, und zu dem Raumgebiet ein ‚offizieller ORTSNAME‘.
Wie bekannt, spielen weitere Eigenschaften wie ‚Geschlecht‘ und ‚Alter‘ eine wichtige Rolle für die möglichen ‚Bedürfnisse‘ der Einwohner. Diese Eigenschaften werden bis auf weiteres ausgeblendet.
FIKTIV oder EMPIRISCH
Im einfachen Fall kann man die Beschreibung einer Ausgangslage ‚fiktiv‘ halten, d.h. man lässt offen, ob es sich um Angaben handelt, die sich ‚empirisch‘ verifizieren lassen, oder die Beschreibung verbindet sich mit einem ‚empirischen Beschreibungsanspruch‘.
Bei einer Ausgangslage mit einem ‚empirischen Beschreibungsanspruch‘ handelt es sich um einen ‚Text‘, für dessen ‚Bedeutung‘ es entsprechende ‚reale Sachverhalte‘ gibt, die jeder persönlich ‚überprüfen‘ kann. Damit dieser Anspruch eingelöst werden kann, muss klar sein, wie eine solche Überprüfung aussehen kann.
Als ‚Standardfall‘ der Überprüfung eines Textes wird hier eine alltägliche Situation angenommen, in der sich jeder Bürger mit seinen ‚normalen Sinnesorganen‘ (Sehen, Hören, Tasten, Riechen, Schmecken,…) davon überzeugen kann, dass jene ‚Wahrnehmungseigenschaften‘ vorliegen, die im Text sprachlich zum Ausdruck gebracht werden, und denen alle beteiligten Bürger ‚zustimmen‘.
Im ‚erweiterten‘ Überprüfungsfall können spezielle ‚Wahrnehmungsgeräte‘ hinzukommen (Lupe, Mikroskop, Fernglas, Fotoapparat, …) oder ‚Messgeräte‘ im Kontext eines ‚Messverfahrens‘. Ein ‚Messverfahren‘ liegt vor, wenn es vereinbarte ‚Standard-Objekte‘ gibt (z.B. ein Gewichtsstandard, ein Längenstandard, ein Temperaturstandard, …), mit deren Hilfe man nach einem bestimmten ‚transparenten‘ Verfahren und ‚von jedem wiederholbar‘ zu einem ‚Messwert‘ kommen kann, der aufgeschrieben werden kann (z.B. ‚5 kg‘, ‚4,4 m‘, ‚17.3 oC‘, …).
Fiktiver Fall
Für Spiele reichen of ‚fiktive Fälle‘, um die Grundidee durchspielen zu können.
So kann man in einer fiktiven Ausgangslage z.B. ‚irgendeine‘ Bevölkerung beschreiben mit folgenden Eigenschaften:
- Es gibt den fiktiven Ort mit Namen ‚ADORF‘.
- Die Einwohnerzahl EINWOHNER betrug im JAHR 2000 genau 1110.
Veränderungsannahmen
Analog kann es bei den Veränderungsannahmen auch ‚fiktive‘ Annahmen geben oder solche mit einem ‚empirischen Geltungsanspruch‘. Hier sei auch zunächst ein fiktiver Fall angenommen.
In diesem fiktiven Beispiel können sich die jährlichen Raten für Zunahme bzw. für Abnahme zufallsgesteuert um einen bestimmten Betrag erhöhen oder vermindern.
- Die jährliche GEBURTENRATE führte zu einem jährlichen ZUWACHS von 0.05 (= 5%)
- Die jährliche STERBERATE führte zu einer jährlichen ABNAHME von 0.06 (= 6%)
- Ein Zufallsereignis GEBURTEN-Rand kann den jährlichen Zuwachs um +/- 0.01 erhöhen oder vermindern.
- Ein Zufallsereignis STERBERATE-Rand kann den jährlichen Zuwachs um +/- 0.01 erhöhen oder vermindern.
- Die komplette Veränderungsregel lautet: EINWOHNER=EINWOHNER+(EINWOHNER * GEBURTENRATE) – (EINWOHNER * STERBERATE)
Regelanwendung
Im Fall des Spiels geht es um die gesamte ‚Spielanleitung‘. Diese beschreibt, wer was wann wie tun kann.
Eine einfache Variante könnte wie folgt gehen:
- Es können beliebig viele Spieler spielen.
- Standardmäßig ist jeder Spieler für eine Bevölkerung verantwortlich. Es kann aber auch vereinbart werden, dass ein Spieler für mehr als eine Bevölkerungen verantwortlich ist.
- Standardmäßig hat eine Bevölkerung zu Beginn 1000 Mitglieder. Es kann aber auch eine andere Zahl vereinbart werden.
- Das Spiel wird in Runden gespielt: In jeder Runde muss jeder Spieler einmal seine Bevölkerung verwalten. Zu Beginn wird festgelegt, wie viele Runden gespielt werden soll.
- Verwalten heißt:
- Beim ersten Mal würfeln stehen die ‚geraden Zahlen‘ für Zunahme und die ‚ungeraden Zahlen‘ für Abnahme.
- Beim zweiten Mal würfeln stehen die Zahlen jeweils für die Werte:
| 1 | 0,01 |
| 2 | 0,02 |
| 3 | 0,03 |
| 4 | 0,04 |
| 5 | 0,05 |
| 6 | 0,06 |
- Wenn die Raten für ‚Erhöhung‘ und ‚Verminderung‘ ermittelt worden sind, wird die Gesamt-Veränderungs-Regel angewendet. Der Betrag für die neue Bevölkerungszahl bildet den Ausgangspunkt für die nächste Runde.
- Die Veränderungen bleiben so lange wirksam, bis ein neuer Wert erwürfelt wurde.
- Gewonnen hat die Bevölkerung, die am Ende die meisten Mitglieder zählt.
Ein Beispiel
(Das folgende Beispiel wurde mit einem Rechenblatt mit der Software ‚libreoffice‘ (Download hier: https://de.libreoffice.org/download/download/) erstellt. Viele andere Programme sind dazu ebenfalls geeignet. Wir werden solche noch vorstellen. )
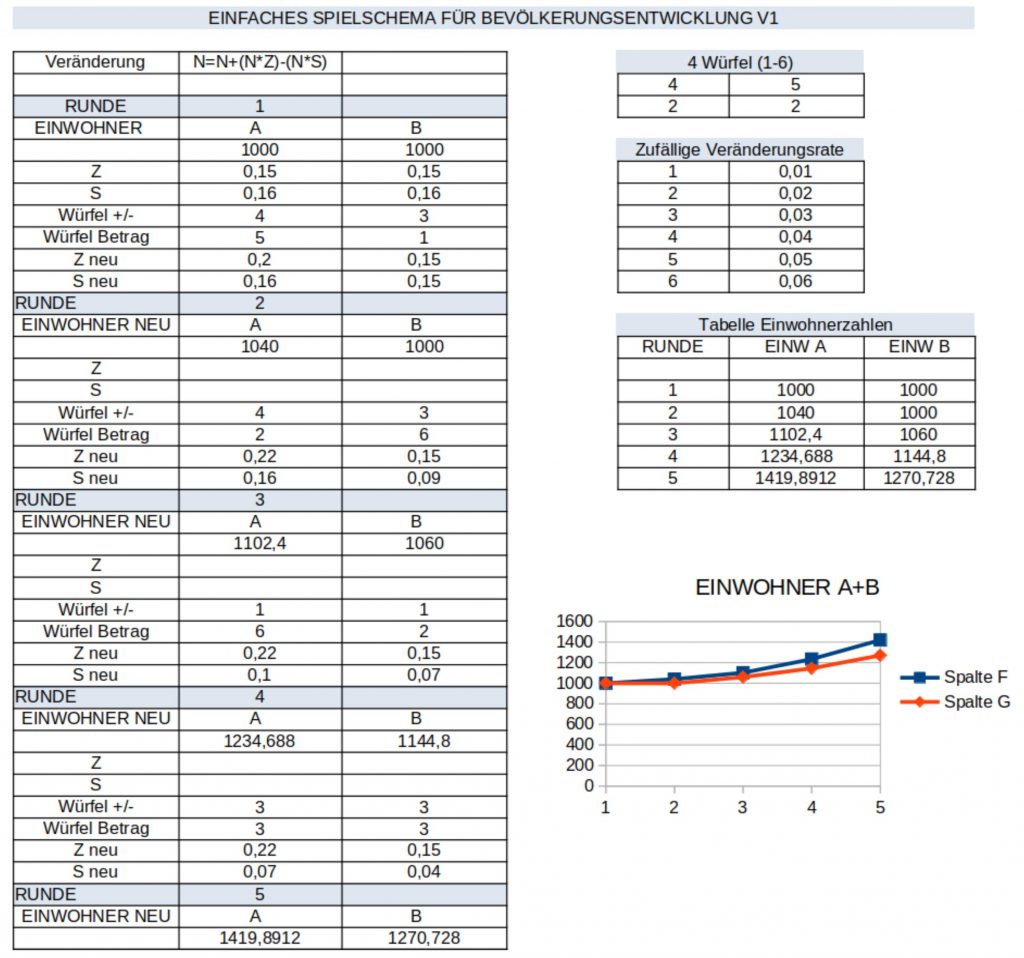
Das Original des Rechenblatts kann man sich hier herunter laden:
Dieses einfache Beispiel mit zwei Spielern mit jeweils einer Bevölkerung A und B zeigt, dass durch die Einbeziehung eines kleinen Zufallsfaktors bei den Raten für Zuwachs (hier nur Geburten) bzw. Abnahme (hier nur Sterbefälle) die Entwicklung der Einwohnerzahlen bei gleichen Startbedingungen auseinander laufen kann.
Bewertung mittels Präferenzen
Wie oben schon angedeutet, kann eine empirische Theorie — auch im Spielformat! — zwar mögliche Fortsetzungen der Gegenwart auf der Basis des aktuell verfügbaren Veränderungs-Wissens aufzeigen, eine empirische Theorie kann aber nicht bewerten. ‚Bewertungen‘ setzen ‚Kriterien für Bewertungen‘ voraus, die ‚extern zum Vorgang‘ verfügbar sein müssen. Also, in der realen Welt, in der wir leben, geht die Sonne auf; es kann regnen; Pflanzen wachsen auf ihre jeweilige Art; Gegenstände fallen von oben nach unten; Wälder können im Sommer oder bei Unwettern (Blitze) brennen; usw. Dies passiert, weil die ‚Welt ist wie sie ist‘ (leicht vereinfacht ausgedrückt).
Dass z.B. ein Wald brennt oder die Flüsse austrocknen kann einfach passieren. Für sich gesehen ist dies weder ‚gut‘ noch ’schlecht‘. Wenn aber z.B. ‚Tiere‘ im Wald leben oder ‚Menschen‘ ihre Häuser in den Wald gebaut haben, dann ist es sehr wahrscheinlich, dass die Menschen mit ihren Häusern im Wald einen Waldbrand nicht ’neutral‘ sehen: sie fühlen sich in ihrer Existenz getroffen und finden dass ein Waldbrand ‚extrem unerwünscht‘ ist. Entsprechend bei starken Regenfällen (Überflutungen), bei Trockenheiten im Sommer, die Pflanzen, Futter vertrocknen lässt, Vieh leidet, Menschen haben weniger oder gar nichts mehr zum Essen. In all diesen Fällen werden die betroffenen Menschen all diese Vorgänge sehr ’negativ‘ empfinden.[3]
Mit diesen wenigen Beispielen wird deutlich, dass ‚Menschen‘ aufgrund ihrer ‚Lebenssituation‘ bestimmte Ereignisse und Vorgänge deutlich ’negativ‘ bewerten können (und tatsächlich auch negativ bewerten). Ob man diese ‚Bewertungs-Einstellungen‘ dann mit ‚Werten‘ in Verbindung bringt oder sie schlicht ‚Präferenzen‘ nennt (‚Waldbrand eher nicht‘, ‚Überflutung eher nicht‘, …), ist vielleicht sekundär; wichtig ist aber, dass Menschen, wenn sie sich auf bestimmte Präferenzen geeinigt haben, ihr weiteres ‚Handeln‘ im ‚Lichte der Präferenzen‘ wahrscheinlich anders organisieren. Gegen Überflutung werden Schutzeinrichtungen (z.B. Dämme) gebaut; Gegen Waldbrände werden z.B. Warnsysteme und Löschmaßnahmen vorbereitet; gegen drohende Dürren beobachtet man bislang eine seltsame Untätigkeit; usw.
Gleichzeitig lehrt uns die wahre Geschichte, dass Präferenzen als solche noch kein gutes Handeln garantieren, da das Handeln, mit dem eine Präferenz umgesetzt werden soll, auf mangelhaftem oder falschem Wissen beruhen kann (eine lange Liste von Beispielen mag sich jeder selbst zusammen stellen).
Angewendet auf das fiktive Beispiel mit den beiden Bevölkerungen A und B heißt dies, dass jene Bürger, die sich mit der Bevölkerungsentwicklung beschäftigen, sich darüber klar werden müssen, was sie von der jeweiligen Entwicklung halten. Finden sie eine Zunahme der Größe der Bevölkerung ‚gut‘ oder eher ’nicht gut‘? Wenn ’nicht gut‘, warum nicht? Welche Faktoren schätzen sie als ’negativ‘ ein?
Im fiktiven Beispiel könnte der Zufallsfaktor, der den ‚Zuwachs‘ oder die ‚Abnahme‘ verändern kann [2], für Unruhe sorgen, falls diese Änderungen in ihrem Umfang konkrete Strukturen in der Gemeinde bedrohen. In diesem Fall müssten die Bürger darüber nachdenken, was man tun könnte, um die Schwankungen im Zuwachs bzw. in der Abnahme besser ‚in den Griff‘ zu bekommen.
Letztlich kann man schon aus diesem einfachen fiktiven Beispiel erkennen, dass ’spielerische Formen der Darstellung‘ sehr wohl geeignet sind, allen Beteiligten ‚hautnah‘ jene ‚Probleme‘ vor Augen zu führen, die in alltäglichen Abläufen ‚verborgen‘ sein können. Ferner bieten spielerische Kontexte direkt auch die Möglichkeit, ‚kreativ‘ über mögliche Voraussetzungen und mögliche Änderungen nachzudenken, und zwar gemeinsam, mit allen anderen.
ANMERKUNGEN
[1] Siehe: https://www.oksimo.org/2023/04/11/grundbegriffe-nachhaltige-entwicklung-empirische-theorie-kommune-spielen/
[2] was es in jeder realen Gemeinde gibt.
[3] Tiere werden dies nicht anders sehen; allerdings haben Tiere keine Stimme unter den Menschen; sie können keine gemeinsamen Beschlüsse fassen, wie sie ihr Umgebung vor solchen Katastrophen schützen.
