Letzte Änderung: 10.März 2024
Autor: Gerd Doeben-Henisch
Kontakt: big-wasser@oksimo.org
–!! Wird noch weiter bearbeitet werden !!–
KONTEXT
Dieser Text gehört zum Themenfeld MODELLE (THEORIEN).
Überblick
In diesem Text findet sich folgender Inhalt:
- Ergebnisse bisher: das lokale und das globale Wassersystem.
- Vorgehen: Wissenschaftlicher Ansatz mit Simulation
- Das erste Modell (die erste Theorie)
- Vom Ereignis zum Konzept
- Von Statik zur Dynamik: Veränderungen
- Beispiel 1: Schöneck mit Einwohnern 2011-2023
- Beispiel 2: Schöneck mit Einwohnern 2011-2023 & Privatem Wasserbedarf
- Bsp.3 : Die Brunnen von Schöneck (mit Grundwasserpegel)
- Bsp.4: Schöneck – Einwohner – Wasserbedarf – Wasserangebot
- Bsp.5: Netzeinspeisung Schöneck
- Bsp.6: Wassermenge im MKK-Wassernetz
- Bsp.7: Private Brunnen im MKK
- Was jetzt zu tun ist
1. Ergebnisse bisher: lokales und globales Wassersystem
Auf der ‚Suche nach dem Wasser‘ hat sich der Gegenstandsbereich für mögliche Daten immer weiter ausgedehnt. Eine aktuelle Skizze des Datenbereichs sieht wie folgt aus:
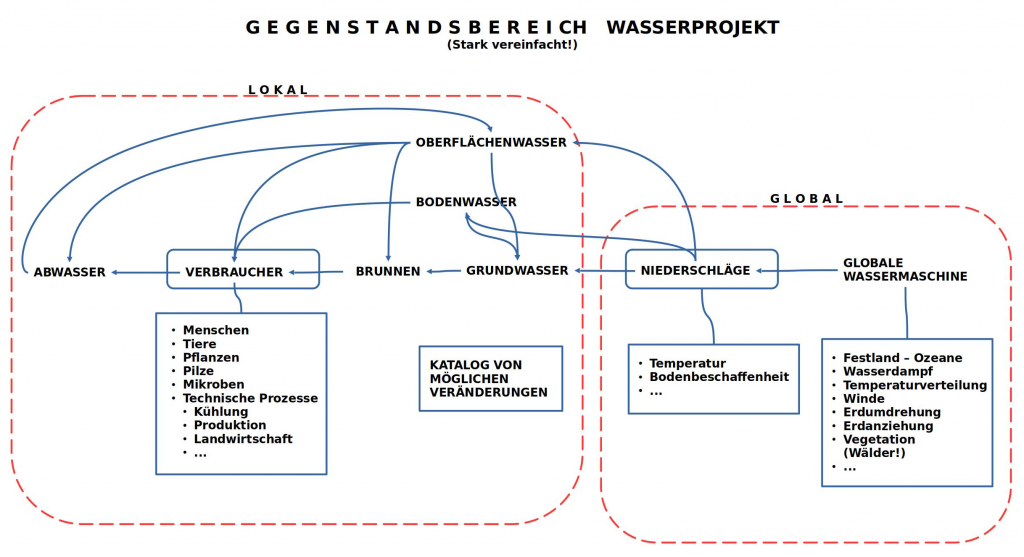
Wie man schon ahnen kann, ist das Thema Wasser ’nicht so ganz ohne‘. Verfolgt man den Weg zurück vom Wasserhahn über das Wasserrohr-System hin zu Hochbehältern und dann Brunnen, dann stößt man unweigerlich auf den schwer fassbaren Grundwasserkörper, der sich im Untergrund auf vielfältige Weise verteilt. Dazu das Oberflächenwaser. In der Zeichnung wird dies alles zum lokalen System gerechnet, da wir es mehr oder weniger unter Kontrolle haben. Was wir fast gar nicht unter Kontrolle haben, das sind die Niederschläge und die Temperatur. Da alles Wasser letztlich aus den Niederschlägen resultiert, hängen wir über die Niederschlägen an einem globalen System, das komplexer nicht sein kann.[4-11]
Im geplanten Erklärungs-Modell soll beides berücksichtigt werden: einmal das lokale System des Wassers und seine Wechselwirkung mit dem globalen System.
Heute geht es zunächst nur mal um die Einführung eines ersten kleinen Modells, anhand dessen man verstehen kann, wie das Ganze überhaupt funktionieren kann.
2. Wissenschaftliches Vorgehen
Das folgende Schaubild gibt einen in Form einer Skizze einen Überblick über das Vorgehen, um zu verstehen, wie alles mit allem zusammenhängt und wie hier Prognosen möglich sein können.
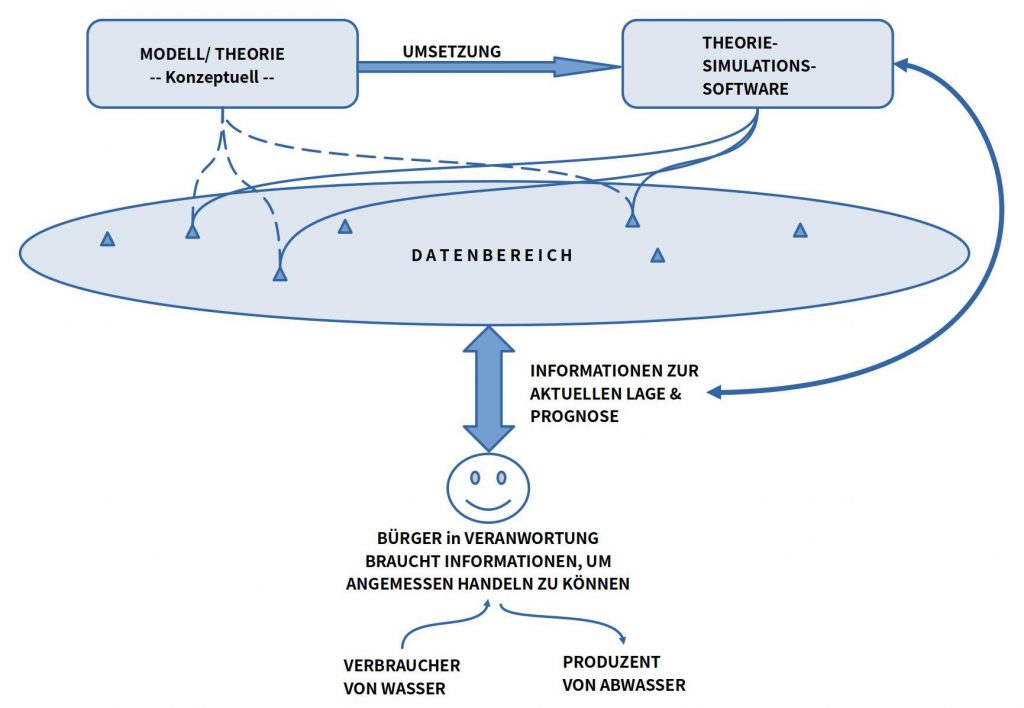
Das oberste Ziel des Projektes ist die Bereitstellung wichtigen Informationen zur aktuellen Lage der Wasserversorgung wie auch eine Prognose, wie sich die Versorgungslage für einen gewählten Zeitabschnitt entwickeln kann.
Eine solche Information ist eine unverzichtbare Voraussetzung für einen Bürger, als Staatsbürger verantwortlich handeln zu können, insbesondere in der Frage der Wasserverfügbarkeit. Diese betrifft nicht nur einzelne Personen, sondern nahezu alle gleichzeitig. Außerdem kann die Versorgungslage ein Handeln erfordern, das langfristige Prozesse erfordert, die möglichst frühzeitig eingeleitet werden müssen.
Damit diese wichtige Information für den Bürger bereit gestellt werden kann, müssen alle Daten erfasst werden, die dafür einschlägig sind. Um hier die ‚Spreu vom Weizen‘ trennen zu können, benötigt man leistungsfähige Konzepte, welche Daten man wie sammelt, aufbereitet und im Rahmen eines Modells/ einer Theorie verarbeitet.
Konzepte/ Theorien können zwar die Dinge klären, real ausrechnen und prognostizieren kann man damit aber nicht. Dazu braucht es eine geeignete Software, die ein Modell/ eine Theorie vollständig repräsentiert und real ausführbar macht.
Der folgende Text zu Modell/ Theorie Nr.1 soll dazu dienen, dieses Konzept samt einer passenden Simulationssoftware vorzustellen.
Dieser Text kann nur eine Einführung bieten. Die vollständige Ausarbeitung und Umsetzung der Theorie samt Simulationssoftware wird sicher einige Monate dauern. Der schwierigste Part ist dabei nicht einmal die Theorie, sondern die Bereitstellung aller notwendigen Daten.
3. Das erste Modell/ die erste Theorie
Im folgenden Text wird gezeigt, wie man für wichtige Größen aus dem Datenbereich Schöneck und MKK ein erstes Modell (eine erste Theorie) bauen kann.
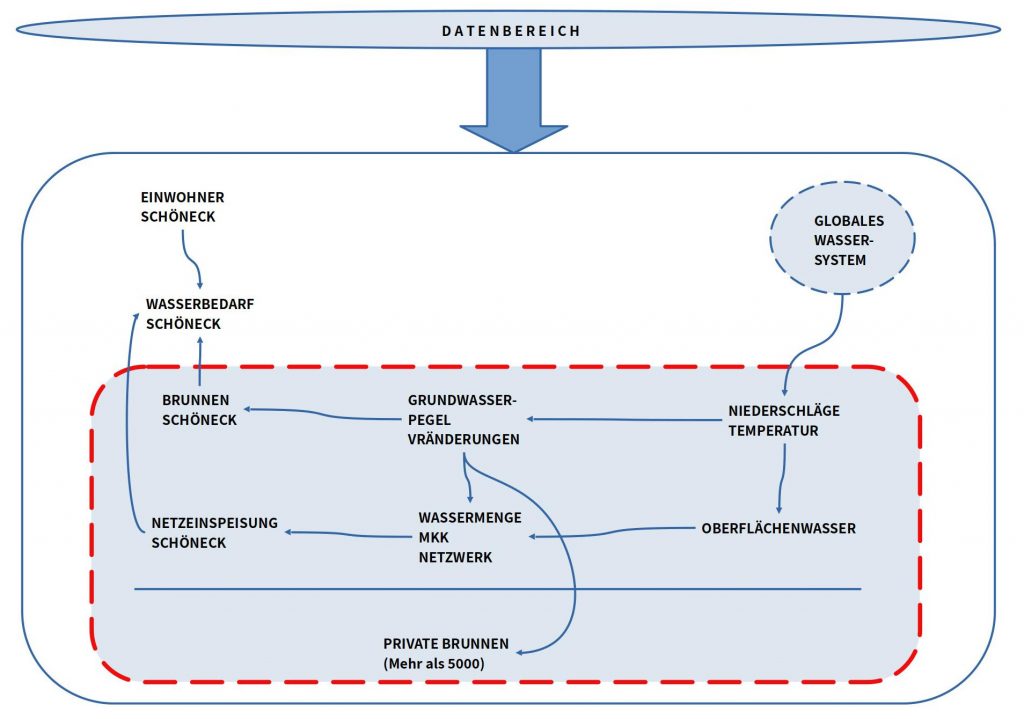
Ausgangspunkt ist der zuvor beschriebene Datenbereich, der ein lokales und ein globales Wasser-System unterscheidet. Das erste Modell fokussiert sich auf das lokale Wasser-System und benutzt vom globalen Wasser-System nur den Output in Form von Niederschlägen und Temperatur.
Innerhalb des lokalen Wasser-Systems werden im ersten Anlauf die folgenden Größen berücksichtigt:
- Die Einwohner von Schöneck (Anzahl, Einbeziehung einer ersten einfachen Dynamik)
- Der Wasserbedarf der Einwohner von Schöneck (nur privater Verbrauch, Mittelwerte)
- Die drei Brunnen von Schöneck (idealisierte Kapazitäten, einfache Dynamik über Grundwasserpegel, abhängig von Niederschlägen und Temperatur)
- Die Netzeinspeisung für Schöneck (reale Werte aktuell unbekannt, aber deutlich größer Null)
- Die Wassermenge, die sich im MKK-Wassernetzwerk befindet (reale Werte aktuell unbekannt, stark schwankend; teilweise auch Nutzung von Oberflächenwasser)
- Private Brunnen (mehr als 5000 im MKK; Verbrauch unbekannt; hohes Gefährdungspotential für Grundwasser)
Vom Ereignis zum Konzept
Das folgende Schaubild illustriert die wichtigsten Elemente einer Beschreibung von Beobachtungen, wenn diese für eine Prognose nutzbar gemacht werden sollen.
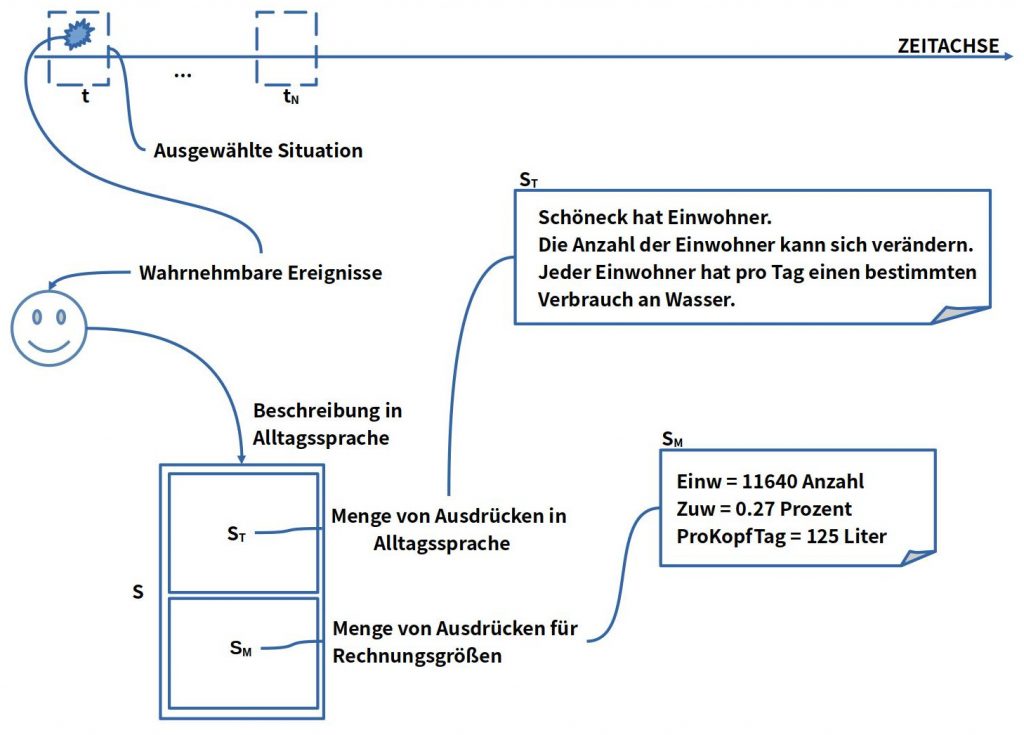
BILD : Skizze zu den Elementen, die für eine Prognose benötigt werden.
Ausgangspunkt für eine Prognose sind Bürger, die sich darauf einigen können, welchen Ausschnitt ihres Alltags sie betrachten wollen. Für eine Auswahl spielt die Zeit eine Rolle, und zwar genauer, ein Zeitfenster. Bürger sind in der Lage, in einem vereinbarten Ausschnitt in einem bestimmten Zeitfenster Sachverhalte und Ereignisse zu beobachten. All das, was sie im Rahmen ihrer Beobachtungen wahrnehmen können, können sie auch mit den Mitteln ihrer Alltagssprache aussprechen und aufschreiben. Jener Teil der Beschreibung, der keine mathematischen Ausdrücke M enthält, sondern nur normale Ausdrücke der Alltagssprache T, wird hier der Textteil ST der Beschreibung S genannt, und jener Teil, der mathematische Ausdrücke M enthält, der mathematische Teil SM der Beschreibung S.
Wie gesagt, das Zeitfenster einer Beobachtung ist wichtig, da beim Voranschreiten der Zeit Veränderungen beobachtet werden können.
Von Statik zu Dynamik: Veränderungen
Der Übergang von rein statischen Beschreibungen zu dynamischen Beschreibungen wird im folgenden Schaubild illustriert.
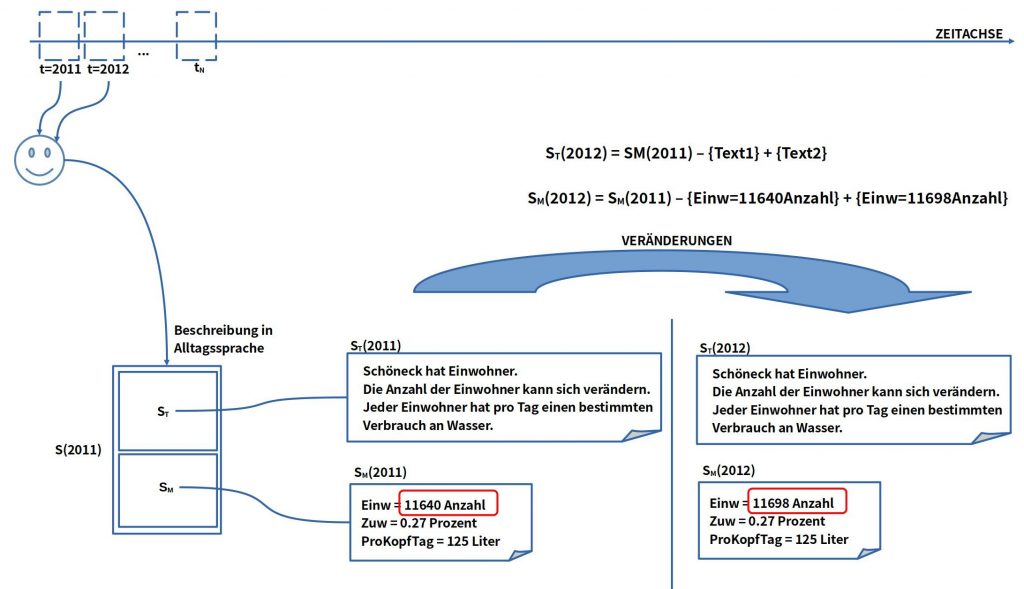
In diesem Schaubild wird angenommen, dass das erste Zeitfenster im Jahr t=2011 liegt, und das nächste Zeitfenster im Folgejahr t=2012.
Während der Textteil ST(2012) der gleiche ist wie ST(2011), also keine Veränderung erkennbar sind, kann man sehen, dass im mathematischen Teil SM() bei der Anzahl der Einwohner ein neuer Wert vorliegt: SM(2012): Einw = 11698 Anzahl.
Während die einzelnen Situationsbeschreibungen S(2011) und S(2012) für sich genommen keine Veränderungen erkennen lassen, so enthüllt der Vergleich, dass es Veränderungen gibt.
Fragt sich, wie kann man Veränderungen beschreiben, wenn die Situationsbeschreibungen jeweils für sich statisch sind?
Wir Menschen sind im Alltag in der Lage, nicht nur aktuelle Situationen wahrzunehmen, wir können auch vergangene Situationen erinnern. Zusätzlich sind wir in der Lage Gegenwärtiges und Erinnertes zu vergleichen. Und das, was wir durch einen Vergleich an Veränderungen erkennen, können wir aussprechen oder aufschreiben.
Im Beispiel hat sich die Anzahl der Einwohner von 2011 zu 2012 verändert. Man könnte also schreiben:
SM(2012) = SM(2011) – {Einw=11640Anzahl} + {Einw=11698Anzahl}
Dies bedeutet, dass aus der Menge der mathematischen Ausdrücke zum Zeitpunkt t=2011 der Ausdruck Einw=11640Anzahl entfernt und ersetzt wird durch den Ausdruck Einw=11698Anzahl, der dann in der neuen Beschreibung S(2012) sichtbar wird.
Man kann aus diesem einfachen Beispiel schon entnehmen, dass man unterscheiden muss zwischen solchen Beschreibungen, die statische Situationen zu einem bestimmten Zeitpunkt beschreiben (hier abgekürzt mit S), und solchen Beschreibungen, in denen Veränderungen beschrieben werden (hier abgekürzt mit V). Es deutet sich damit an, dass wir bei der Beschreibung unseres Alltags mindestens diese zwei Komponenten brauchen werden: S und V. Fragt sich nur, wie man diese beiden Komponenten zusammenbringen kann?
Erinnern wir uns für einen Moment an Spiele, genauer Brettspiele, und hier an das Spiel Mensch ärgere dich nicht.
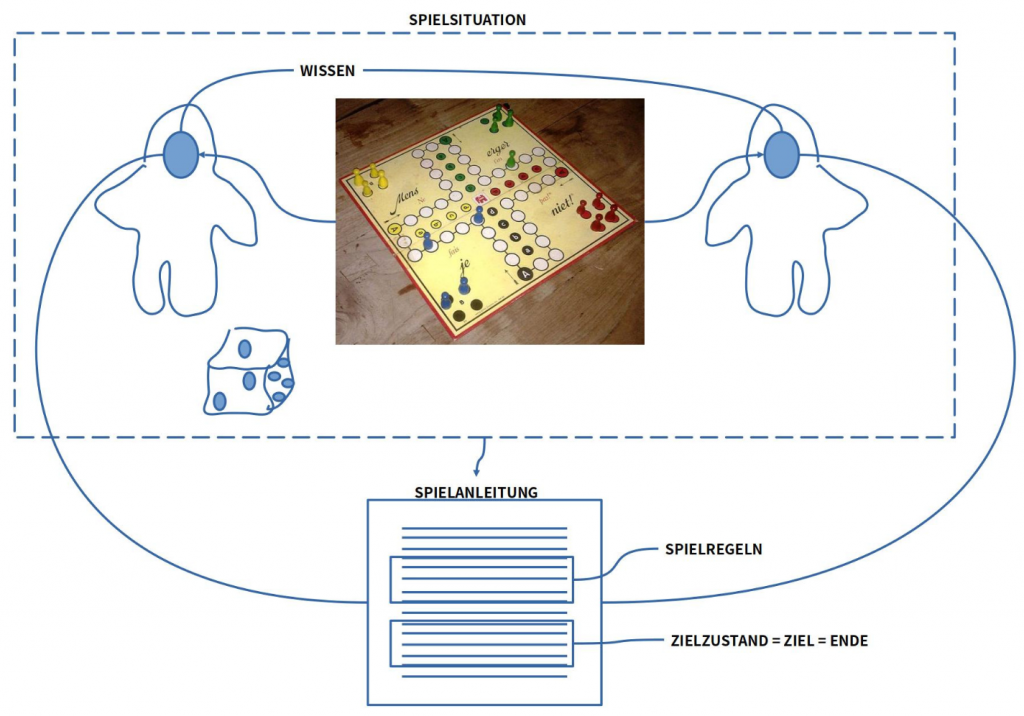
Beim Spiel ‚Mensch ärgere dich nicht‘ besteht eine Situation aus dem Spielbrett mit Symbolen und Spielsteinen, dazu die Spieler und ein Würfel. Mögliche Veränderungen werden in den Spielregeln beschrieben. Die Spielregeln alleine sagen aber nicht, wer wann welche Regel wie anwenden darf. Dazu gibt es eine Spielanleitung, die genau das beschreibt. Diese Spielanleitung (samt den Regeln) muss jeder kennen, sonst kann das Spiel nicht stattfinden.
Daraus ergibt sich, man benötigt zu einem Spielprozess in der Zeit eine Ausgangslage (Brett, Spielsteine, Spieler, Würfel) (S), dazu Spielregeln (V), die jeder kennen muss, und eine Anwendungsvorschrift (ANW) anhand deren man weiß, wer wann was tun darf. Man könnte also auch sagen, die Spieler müssen wissen, wie sie eine aktuelle Situation S mit Hilfe von Spielregeln V in eine neue Situation transformieren können. Diese Transformation geschieht durch die Umsetzung einer Anwendungsvorschrift ANW. Man könnte auch schreiben:
SPIELER: ANW(S(t),V) = S(t‘)
Umschrieben: SPIELER sind in der Lage, mit Hilfe einer Anwendungsvorschrift ANW eine Situation S zum Zeitpunkt t mit Hilfe von Veränderungsregeln in eine neue Situation S zum Zeitpunkt t‘ zu transformieren.
In einer normalen wissenschaftlichen Theorie nennt man die Anwendungsvorschrift ANW meistens Folgerungsbegriff oder Ableitungsvorschrift oder Folgerungsmechanismus und bedient sich dazu der Logik. Im Kontext der Logik benutzt man statt der Abkürzung ANW eher das Zeichen ⊢. Dann könnte man schreiben:
SPIELER: (S(t),V) ⊢ S(t‘)
Das Ergebnis einer Folgerung ist heißt dann meistens Ableitung oder Folgerung oder Prognose.
Im Fall von zeitlich geordneten Situationen geht man davon aus, dass man das Ergebnis einer Ableitung — z.B. S(t2) — wieder zum Gegenstand einer Anwendung machen kann, also
SPIELER: ANW(S(t1),V) = S(t2)
SPIELER: ANW(S(t2),V) = S(t3)
usw.
was natürlich voraussetzt, dass die benutzten Veränderungsregeln V dies auch hergeben. Wie man beim Spiel ‚Mensch ärgere Dich nicht‘ sehen kann, geht dies sehr wohl.
Den Fall einer mehrfachen Anwendung ANW einer Anwendungsvorschrift nennt man normalerweise Simulation. Kürzt man die Anwendungsvorschrift ANW ab mit SIM und fügt noch die Anzahl N der gewünschten Simulationsrunden hinzu, dann könnte man verkürzt auch schreiben:
SPIELER: SIM(N)(S(t0)
was ausgeschrieben dann heißen würde
SPIELER: SIM(N)(S(t0),V) = S(t1)
SPIELER: SIM(N)(S(t1),V) = S(t2)
…
SPIELER: SIM(N)(S(tN-1),V) = S(tN)
Beispiel 1: Schöneck mit Einwohnern 2011-2023
Anhand des hessischen statistischen Landesamtes kann man die Einwohnerzahlen von Schöneck für die Zeitpunkte 2011-2022 bekommen. Dabei ist zu beachten, dass die Einwohnerzahl immer am 31. Dezember des betreffenden Jahres festgemacht wird.
| Zeitscheiben | Einwohner insgesamt | Diff | % |
| 2011 | 11.640 | ||
| 2012 | 11.698 | 58 | ,5 |
| 2013 | 11.625 | -73 | -,6 |
| 2014 | 11.668 | 43 | ,4 |
| 2015 | 11.812 | 144 | 1,2 |
| 2016 | 11.926 | 114 | 1,0 |
| 2017 | 11.902 | -24 | -,2 |
| 2018 | 11.864 | -38 | -,3 |
| 2019 | 11.918 | 54 | ,5 |
| 2020 | 11.900 | -18 | -,2 |
| 2021 | 11.853 | -47 | -,4 |
| 2022 | 11.986 | 133 | 1,1 |
| 2023 | 12.700 | 714 | 6,0 |
Die Zeitreihe der prozentualen Veränderung als Kurve:
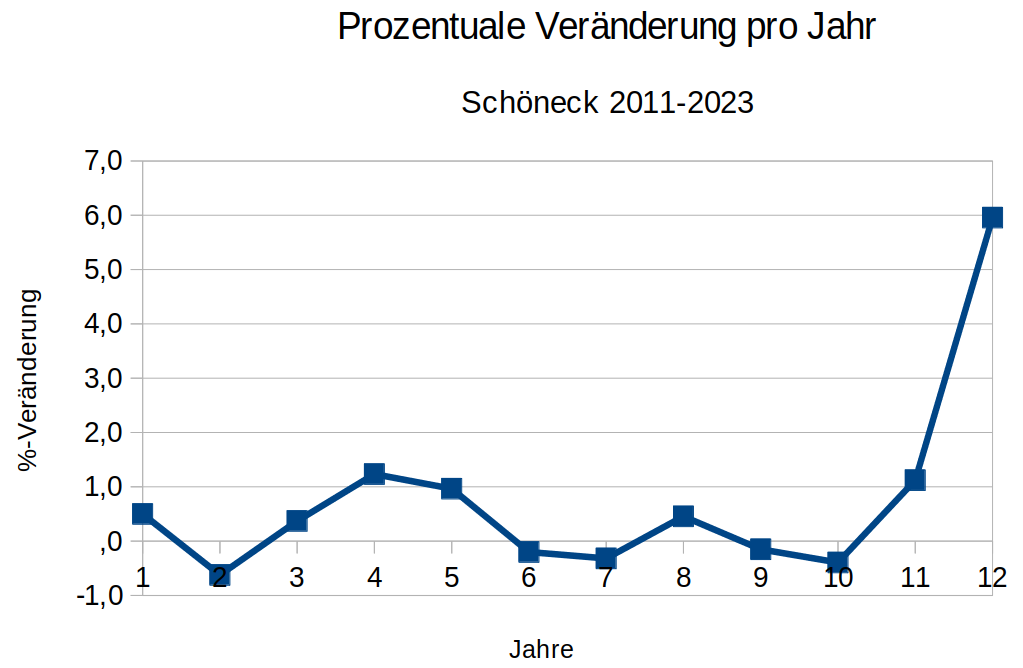
Diese Zeitreihe ist nicht uninteressant: Würde man nur die Jahre 2011 – 2022 betrachten, dann käme man auf einen Mittelwert der prozentualen Veränderung über die Jahr von 0,27 %. Betrachtet man aber die Zeitreihe 2011 – 2023 dann würde sich der Mittelwert nur aufgrund des einen Jahres 2023 auf 0,74% erhöhen. Für eine Prognose würden sich damit deutlich verschiedene Werte ergeben. Welcher Wert wäre der ‚bessere‘?
Da Prognosen Mittelwerte voraussetzen, werden Prognosen im Falle einer unregelmäßigen Zeitreihe schwierig bis unmöglich. Der Fall des Ausreißers im Jahr 2023 deutet an, dass es Faktoren gibt, die die Entwicklung stark beeinflussen können. Dies sei kurz illustriert.
Einen Startzustand S(t=2011) könnte man wie folgt beschreiben:
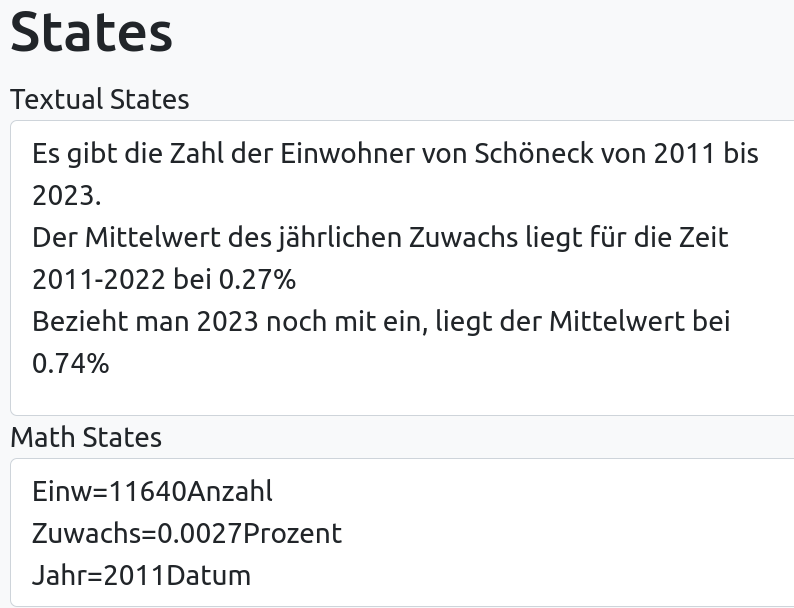
Veränderungsregeln V für den mathematischen Teil des Zustands S(t=2011) könnten wie folgt aussehen:
V1: Einw=Einw+(Einw*Zuwachs)
V2: Jahr=Jahr+1
Wie man hier sehen kann, kann man im mathematischen Teil mehr als eine Veränderungsregel angeben.
Fall Zuwachs 0.27% pro Jahr:


(Zum selber ausprobieren gehe auf https://oksimo.com/public_theories und wähle die Theorie aus: demo-theorie-bsp1 )
Man kann klar erkennen, dass bei dem durchschnittlichen Zuwachs von 0.27% pro Jahr die Voraussage für das Jahr 2022 ziemlich genau ist, aber noch im Jahr 2030 mit der Einwohnerzahl deutlich unter dem Wert liegt, den Schöneck schon 2023 erreicht hatte.
Mir den gleichen Veränderungsregeln kann man auch den Fall simulieren, in dem sich die Größe Zuwachs geändert hat:
Fall Zuwachs 0.74% pro Jahr:


(Zum selber ausprobieren gehe auf https://oksimo.com/public_theories und wähle die Theorie aus: T-einwohner-schoeneck-2011-2023-p0-7 )
Man kann klar erkennen, dass bei dem durchschnittlichen Zuwachs von 0.74% pro Jahr die Voraussage für das Jahr 2023 ziemlich genau ist, und im Jahr 2030 mit der Einwohnerzahl deutlich über dem Wert liegt, den Schöneck schon 2023 erreicht hatte.
Beispiel 2: Schöneck mit Einwohnern 2011-2023 & Privatem Wasserbedarf
Annahmen über den Startzustand S(t=2011)
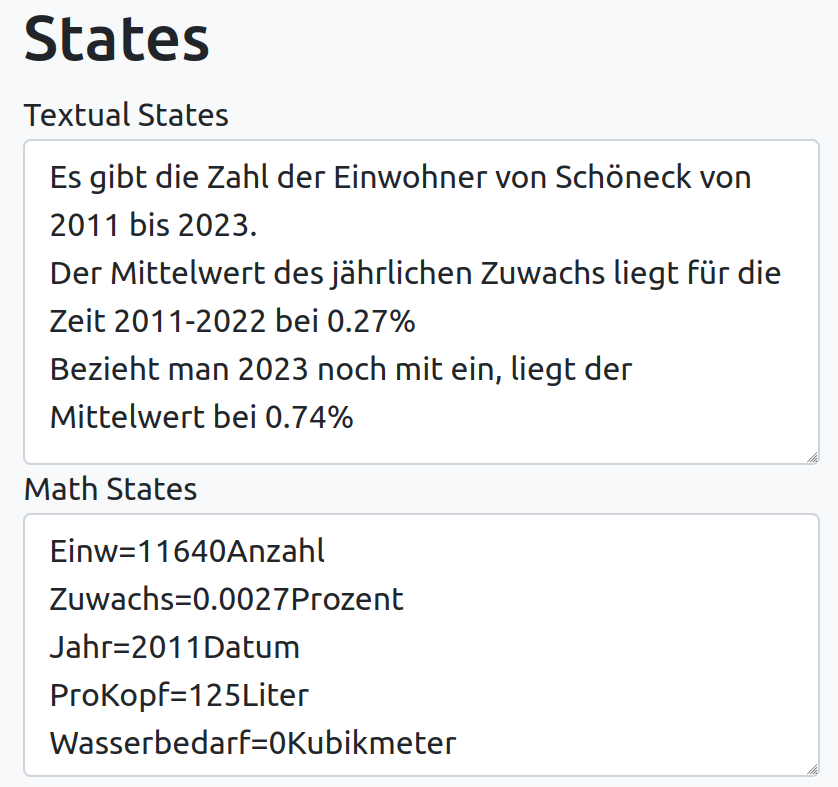
VERÄNDERUNGSREGELN
V1: Einw=Einw+(Einw x Zuwachs)
V2: Wasserbedarf=(Einw x ProKopf*365)/1000
V3: Jahr=Jahr+1
Ausgabe der Werte als Tabelle:

(Zum selber Simulieren auf https://oksimo.com/public_theories gehen und die Theorie demo-theorie-bsp2-einw-wasserbedarf-v1 auswählen.)
Bsp.3 : Die Brunnen von Schöneck
Im folgenden Text wird die Gesamtkapazität der Brunnen von Schöneck beschrieben. [13] Dabei wird zusätzlich der Faktor der Abhängigkeit der Brunnen vom Grundwasserspiegel angenommen.[14,15] Für den Grundwasserpegel gilt die Aussage des Hessischen Landesamtes HLNUG vom Mai 2023, dass der Grundwasserpegel in Hessen in den letzten Jahren um 27% gefallen ist.[12]
Für das erste Modell mit Namen demo-theorie-bsp3ges-brunnen wird mit folgenden Annahmen gearbeitet:
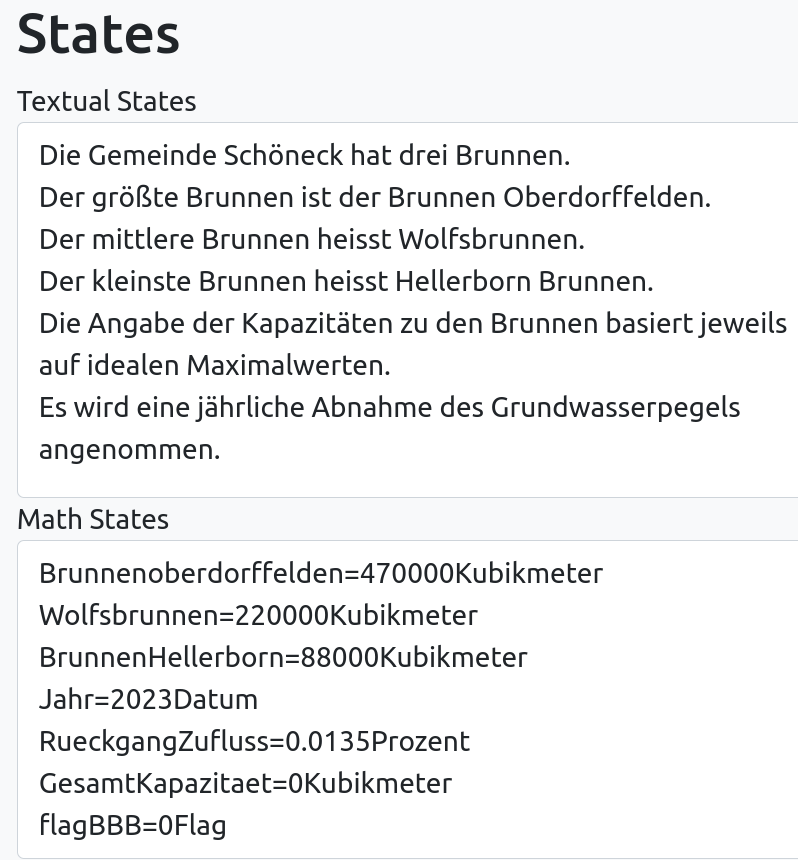
Veränderungsregeln
brunnenoberdorffelden-kapazitaet-aenderung-v1
Brunnenoberdorffelden=… Brunnenoberdorffelden-(Brunnenoberdorffelden*RueckgangZufluss) …
wolfsbrunnenkapazitaet-aenderung-v1
Wolfsbrunnen=… Wolfsbrunnen-(Wolfsbrunnen*RueckgangZufluss) …
Hellerborn-brunnenkapazitaet-aenderung-v1
BrunnenHellerborn=… BrunnenHellerborn-(BrunnenHellerborn*RueckgangZufluss) …
gesamtkapazitaet-v1
GesamtKapazitaet= … Brunnenoberdorffelden+Wolfsbrunnen+BrunnenHellerborn …
SIMULATION
Eine Simulation der Theorie demo-theorie-bsp3ges-brunnen zeigt folgende Werte auf:
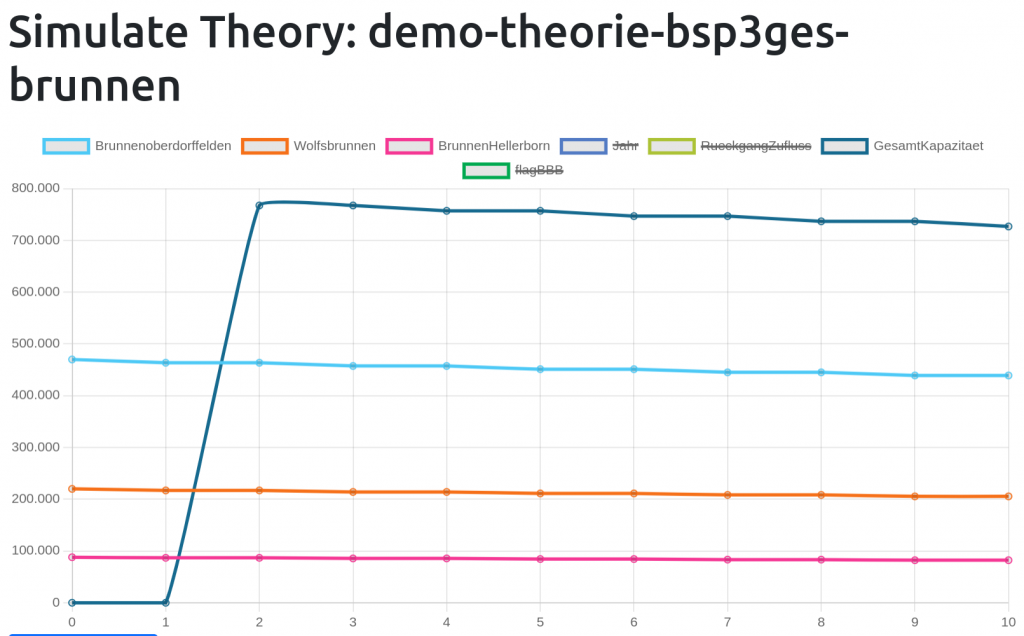
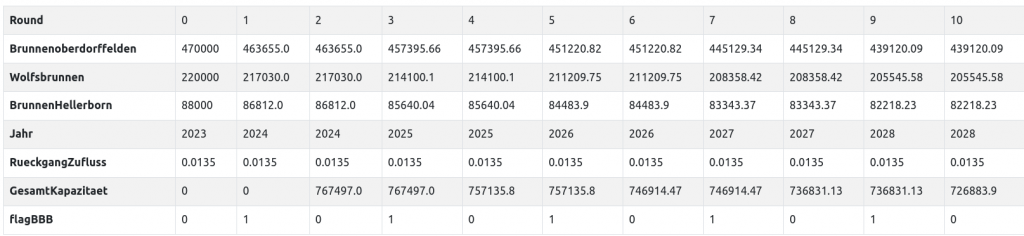
Man kann deutlich sehen, wie die Gesamtkapazität mit diesen Modellannahmen schon in vier Jahren deutlich sinken würde. Allerdings fehlen dringend reale Messwerte der Brunnen und der Grundwasserpegelstände (In der Nachbargemeinde Maintal gibt es seit Jahren 42 Grundwassermessstellen, die alle online sind und in nahezu Echtzeit Grundwasserpegel anzeigen.)
Zum selber ausprobieren der Simulation kann man auf die Seite oksimo.com gehen, dort den Reiter Public Theories anklicken, und dort in der Liste den Namen des Modells anklicken.
Bsp.4: Schöneck – Einwohner – Wasserbedarf – Wasserangebot
Nach diesen Vorarbeiten kann man jetzt die Faktoren Einwohner von Schöneck, Wasserbedarf anhand eines Pro-Kopf-Verbrauchs, und Wasserangebot durch die Brunnen (ohne externe Einspeisung) darstellen.
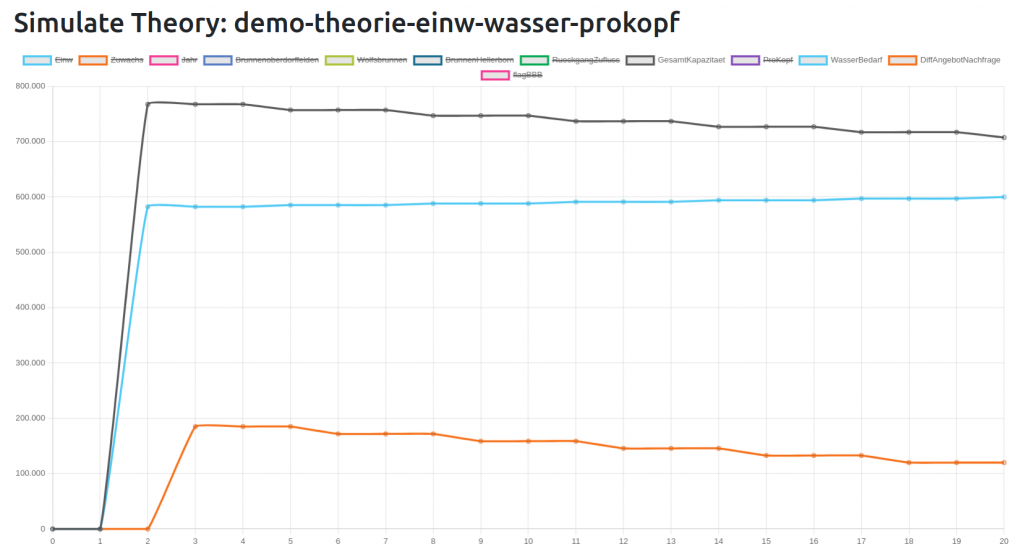
Das folgende Schaubild illustriert die wichtigste Botschaft: Mit den aktuellen Annahmen verkleinert sich der Abstand zwischen Wasser-Angebot und Wasser-Bedarf innerhalb von 6 Jahren auf eine Differenz von 120.000 m3 . Umgelegt auf die Bürger wären das nur noch ca. 21 von 13.151 Bürger, die dann noch versorgt werden könnten.
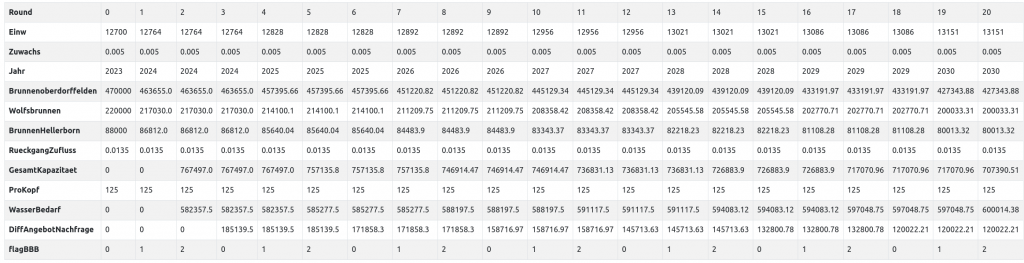
Da die Differenz zwischen Nachfrage und Angebot so abstrakt aussieht, hier eine Veranschaulicht umgerechnet in die Anzahl der Personen, die durch die Reserve noch versorgt werden könnten:
Innerhalb von vier Jahren ab 2024 würde sich die Reserve von ca. 4.000 Bürgern auf ca. 2.900 Bürger von dann 13.000 Einwohnern reduzieren.
Diese Berechnung ist mit der leicht erweiterten Theorie demo-theorie-bsp4b-anz-buerger-noch-wasser möglich.
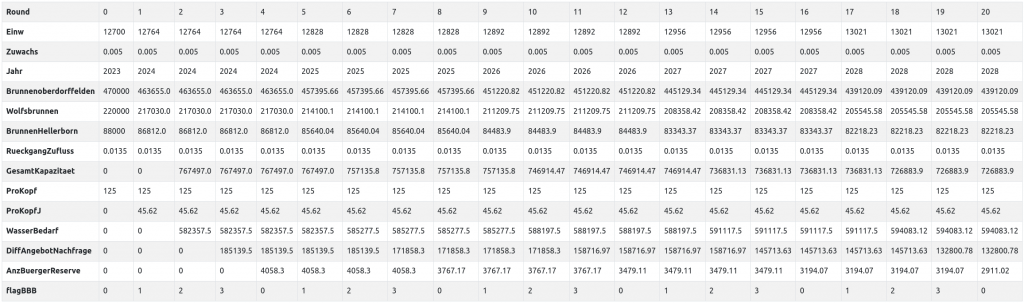
Regel-Hierarchien in der Theorie ‚demo-theorie-einw-wasser-prokopf‘
In der Demo-Theorie ‚demo-theorie-einw-wasser-prokopf‘ wird von einer interessanten Eigenschaft der Software Gebrauch gemacht.
Einige der mathematischen Größen, die in der Theorie benutzt werden (wie z.B. ‚Einw‘, ‚GesamtBedarf‘) können untereinander in einem Abhängigkeitsverhältnis stehen. So etwa in der Formel:
GesamtKapazitaet=… Brunnenoberdorffelden+Wolfsbrunnen+BrunnenHellerborn
Dies bedeutet, damit der Wert der Größe ‚GesamtKapazitaet‘ berechnet werden kann, müssen zuvor die Werte der Größen ‚Brunnenoberdorffelden, Wolfsbrunnen, BrunnenHellerborn‘ berechnet worden sein.
Da aber der Folgerungsbegriff der Software oksimo alle Regeln gleichwertig behandelt und sie mit einem Zufallsverfahren anordnet und dann anwendet, kann es passieren, dass erst die Größe GesamtKapazitaet berechnet würde, bevor die Werte Brunnenoberdorffelden, Wolfsbrunnen, BrunnenHellerborn berechnet worden sind.
Um solche Verwirrungen von vornherein auszuschließen, kann man entsprechend den Abhängigkeiten unter den Größen Hierarchie-Ebenen (oder Level) bilden. Dies geschieht z.B. dadurch, dass man eine Glag-Variable einführt — hier flagBBB — die verschiedene Werte annehmen kann — hier: 0,1,2 –, die für einen Level stehen. Dann kann man sagen, welche Regeln sollen bei flag==0, bei flag==1 usw. ausgeführt werden. Auf diese Weise kann man beliebig große Hierarchien einführen. Bei der Wertanzeige in der Tabelle oder im Graph erkennt man das daran, dass eine Simulationsrunde sich über mehrere Positionen erstreckt. Für den Anwender kann dies ein wenig unangenehm sein, für die Konstruktion einer komplexen Theorie ist es aber ungeheuer angenehm.
Vorgabe:
flagBBB=0Flag
Einw-verlauf-bedarf-v1
Wenn: flaggBB==0
Einw=Einw+(eval(„{:.0f}“.format(Einw*Zuwachs)))
Jahr=Jahr+1
brunnenoberdorffelden-kapazitaet-aenderung-v1
Wenn: flagBBB==0
Brunnenoberdorffelden=eval(„{:.2f}“.format(Brunnenoberdorffelden-(Brunnenoberdorffelden*RueckgangZufluss)))
wolfsbrunnenkapazitaet-aenderung-v1
Wenn: flaggBBB==0
Wolfsbrunnen=eval(„{:.2f}“.format(Wolfsbrunnen-(Wolfsbrunnen*RueckgangZufluss)))
Hellerborn-brunnenkapazitaet-aenderung-v1
Wenn: flaggBB==0
BrunnenHellerborn=eval(„{:.2f}“.format(BrunnenHellerborn-(BrunnenHellerborn*RueckgangZufluss)))
Aktiviere-gesamtkapazitaet-v1
Wenn: flagBBB=0
Dann: flagBBB=1
gesamtkapazitaet-v1
Wenn: flagBBB==1
WasserBedarf=eval(„{:.2f}“.format(Einw*ProKopf*365)/1000))
GesamtKapazitaet=eval(„{:.2f}“.format(Brunnenoberdorffelden+Wolfsbrunnen+BrunnenHellerborn))
flagBBB=2
differenz-ang-nachfrage
Wenn: flagBBB==2
DiffAngebotNachfrage=eval(„{:.2f}“.format(GesamtKapazitaet-WasserBedarf))
flagBBB=0
Bsp.5: Netzeinspeisung Schöneck
In den bisherigen Annahmen wurde idealisierend davon ausgegangen, dass Schöneck nur über die drei genannten Brunnen verfügt und dass diese maximal liefern. Beides ist unrealistisch. Real liefern die drei Brunnen weniger Wasser (genau Daten müssen erhoben werden) und über die Wasser-Netz-Verbindungen ist Schöneck mit dem gesamten Netz der MKK-Wasserwerke verbunden (siehe Schaubild aus [16], S.15).
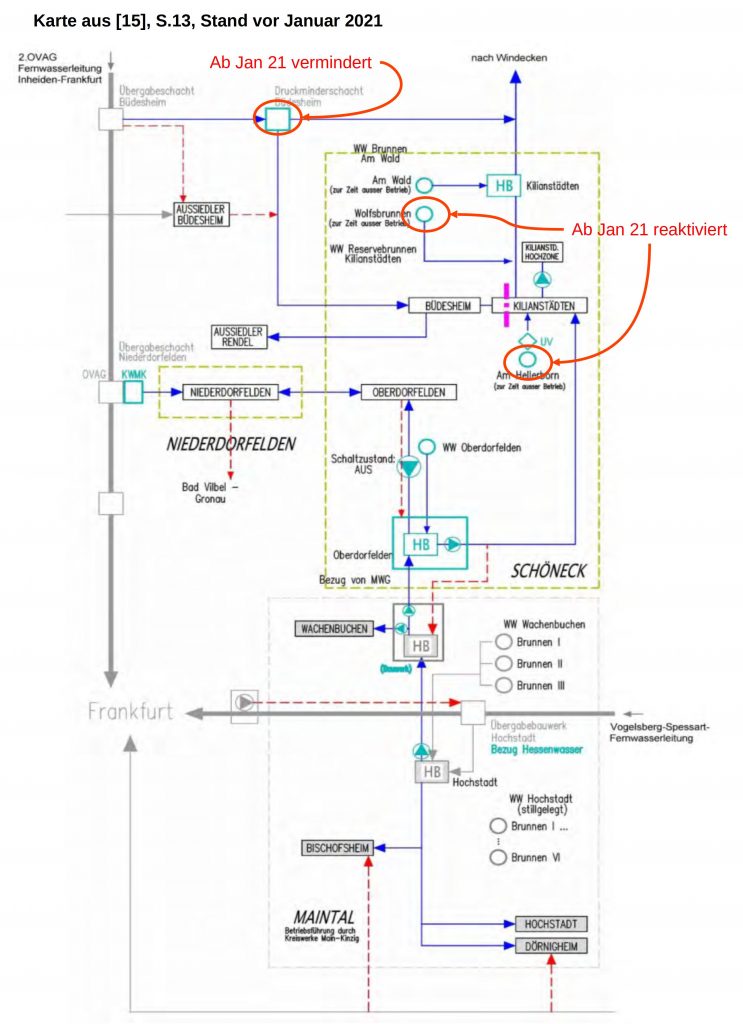
Genaue aktuelle Zahlen liegen nicht vor. Zusätzlich ist zu berücksichtigen, dass die Gemeinde Niederdorffelden mit der Gemeinde Schöneck als Einheit zu sehen ist, da Niederdorffelden keinerlei eigene Wasserwerke besitzt.
Hier besteht erheblicher Klärungsbedarf.
Bsp.6: Wassermenge im MKK-Wassernetz
Dadurch, dass die Wasserversorgung von Schöneck mit Niederdorffelden aus eigenen Mittel nicht ausreicht, stellt die Verbindung zum MKK Wassernetzwerk einen essentiellen Faktor dar. Daraus stellt sich die Frage, in welchem Umfang denn die verfügbare Menge Wasser für das MKK Wassernetzwerk (i) für die Versorgung von Schöneck-Niederdorffelden gesichert ist und (ii) für welchen Zeitraum.
Wenn man weiß, dass das MKK Wassernetzwerk in den Jahren 2009 – 2020 zu ca. 40% von externen Lieferungen abhing [16, S.16], dann kann das entweder beruhigend wirken, weil es eine Unterstützung gibt, es kann aber auch beunruhigen, da hier eine große Unbekannt vorliegt.
Die Frage der verfügbaren Wassermenge des MKK Wassernetzwerks sollte also geklärt werden.
Bsp.7: Private Brunnen im MKK
Aufgrund von privaten Recherchen muss davon ausgegangen werden, dass es im Bereich des MKK über 5000 private Brunnen gibt. Diese werden weder hinsichtlich der tatsächlichen Entnahmen noch hinsichtlich von Sicherheitsmaßnahmen gegen Verschmutzungen kontrolliert. Während viele Brunnen (wie viele?) nur kleine Brunnen für den privaten Gebrauch sind, gibt es auch größere Brunnen (es soll Brunnen mit Tiefen bis zu 200 m geben), die für den Grundwasserkörper erhebliche Gefahren darstellen können. Da private Brunnen bis zu 3.600 m3/Jahr fördern dürfen, könnten dies immerhin 18 Mio m3 Wasser/ Jahr sein. Bedenkt man, dass das MKK Wassernetzwerk in 2020 selbst nur 3.8 Mio m3 gefördert hat, würde die private Förderung ca. das 4.7fache der offiziellen Förderung ausmachen. Bei einer zunehmenden Knappheit der Grundwasserverfügbarkeit muss man sich möglicherweise die Frage stellen, wie der Main-Kinzig Kreis mit diesem Faktor umgeht. Immerhin ist nicht ausgeschlossen, dass aus den Brunnen — zumindest auch bei den größeren Brunnen — erheblich mehr Volumen als 3.600 m3 gefördert werden.
Was jetzt zu tun ist
Muss noch ausgearbeitet werden.
QUELLEN
[1] Hess. Gemeindestatistik, 2005 – 2023, https://www.statistischebibliothek.de/mir/receive/HESerie_mods_00000449
[2] Schöneck 2024 (Zahlen von 2022!): www.statistikportal.de/gemeindeverzeichnis/06435026
[3] Destatis, Bevölkerungsvorausberechnung: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Bevoelkerungsvorausberechnung/_inhalt.html#sprg233978
[4] Victor Gorshkov , V.V. Gorshkov , A.M. Makariev, Biotic Regulation of the Environment. Key Issues of Global Changes. Springer, 2000
[4b] Fernsehbeitrag: arte.de, 8.Dez 2023, Die fliegenden Flüsse des Amazonas – Zum Film heißt es: Die Wolkenansammlungen über dem Regenwald des Amazonas enthalten riesige Wassermassen, mehr als der Amazonas selbst. Wenn diese „fliegenden Flüsse“ auf die Anden treffen, werden sie in Richtung Süden gedrängt und regnen über den Städten Südamerikas ab. Seit mehr als 20 Jahren erforscht Professor Antonio D. Nobre das Geheimnis dieser Wasserströme in der Atmosphäre. URL: https://www.arte.tv . Anmerkung: Noble benutzt die Theorie von [1]!
[5] DWD: Klimawandel – ein Überblick. Klimaänderungen können auf natürliche sowie auf menschliche Einflüsse zurückgeführt werden. Seit Mitte des 20. Jahrhunderts haben sich die oberflächennahen Luftschichten der Kontinente und Ozeane der Erde deutlich erwärmt. Der Klimawandel zeigt sich in den letzten Jahrzehnten unter anderem in der Zunahme von heißen Temperaturextremen, dem stetigen Anstieg des Meeresspiegels und der mancherorts veränderten Häufigkeit von extremen Niederschlägen. Anthropogene Aktivitäten sind hierfür die Hauptursache.
[6] DWD, 31.01.2024, Meilenstein in der Klima- und Wetterforschung. Wetter- und Klimamodell ICON als Open-Source veröffentlicht
[7] DWD, Deutscher Klimaatlas . Bereich Hessen.
[8] IPCC, 2021, Climate Change 2021: The Physical Science Basis, the Working Group I contribution to the Sixth Assessment Report on 6 August 2021 during the 14th Session of Working Group I and 54th Session of the IPCC. Full Report HERE.
[9] Pierre L. Ibisch, Heike Molitor, Alexander Conrad, Heike Walk, Vanja Spoo (geb. Mihotovic), Juliane Geyer, 2022, Der Mensch im globalen Ökosystem. Eine Einführung in die nachhaltige Entwicklung. 2. Auflage. Zusammenfassung: Als Begriff ist Nachhaltigkeit heute in aller Munde, doch mit der Umsetzung nachhaltiger Wirtschafts- und Gesellschaftsstrukturen tun wir uns nach wie vor schwer. Dieses Buch ist gedacht als Überblick über relevante Diskurse – aber auch und vor allem als Denkangebot mit neuen Vorschlägen für die Verteidigung und weitere Ausgestaltung des Konzeptes der nachhaltigen Entwicklung. Es widmet sich der Position der Menschheit im globalen Welt(öko)system und versteht Nachhaltigkeit disziplinübergreifend. Die Problemanalyse steht dabei ebenso im Zentrum wie Lösungsansätze und die Bedingungen für eine nachhaltige Entwicklung.
Die Hochschule für nachhaltige Entwicklung Eberswalde (HNEE) widmet sich dem Thema der Nachhaltigkeit in Lehre, Forschung, Transfer und Betrieb umfassend und in seiner ganzen Komplexität. Sie war die erste deutsche Hochschule, die ein ausgewiesenes Profil der nachhaltigen Entwicklung in einem breiten Beteiligungsprozess mit den Hochschulangestellten und Studierenden umgesetzt hat und gilt als eine der Leuchtturmhochschulen in Deutschland.
Dieses Lehrbuch ist aus einer fachbereichsübergreifenden Grundvorlesung zur nachhaltigen Entwicklung an der HNEE entstanden. Auf ihrer Grundlage haben die Herausgeber*innen das Buch konzipiert und es mit weiteren Kolleg*innen ausgestaltet.
[10] Kurt Lechner, Hans-Peter Lühr, Ulrich V.E.Zanke (Hrsg.), Taschenbuch der Wasserwirtschaft. Grundlagen – Maßnahmen – Planung, 10.Aufl., 2021, Springer Verlag
[11] Hamburger Bildungsserver, Der globale Wasserkreislauf, https://bildungsserver.hamburg.de/themenschwerpunkte/klimawandel-und-klimafolgen/wasserkreislauf-global-254514
[12] HLNUG, Pressemitteilung: Keine Winterdürre. Grundwasser in Hessen leicht erholt, 16.Mai 2023, URL: https://umwelt.hessen.de/presse/grundwasser-in-hessen-leicht-erholt
[13] Zu Brunnenkapazität Schöneck, siehe Gerd Doeben-Henisch, 23.Nov 23, Welche Faktoren spielen für die Wasserversorgung in Schöneck eine Rolle? dort der Abschnitt FAKTOR: WASSERANGEBOT, mit weiterführender Literatur.
[14] Zu GRUNDWASSER-NEUBILDUNG, siehe Gerd Doeben-Henisch, 23.Nov 23, Welche Faktoren spielen für die Wasserversorgung in Schöneck eine Rolle? dort der Abschnitt FAKTOR: GRUNDWASSER-NEUBILDUNG, mit weiterführender Literatur.
[14b] Grundwassermessstellen in Maintal: https://www.maintal.de/seite/134067/grundwassermessstellen.html
[15] Zum Thema Niederschläge und Temperatur, Gerd Doeben-Henisch, 23.Nov 23, Welche Faktoren spielen für die Wasserversorgung in Schöneck eine Rolle? dort der Abschnitt FAKTOR: NIEDERSCHLÄGE & TEMPERATUR, mit weiterführender Literatur.
[16] BGS UMWELT – Brandt Gerdes Sitzmann Umweltplanung GmbH, Kreiswerke Main-Kinzig GmbH, Brunnen Oberdorfelden, Unterlagen zum Wasserrechtsantrag, https://rp-darmstadt.hessen.de/sites/rp-darmstadt.hessen.de/files/2022-10/bericht_schoeneck.pdf, Projekt 5948-20, Juli 2021, Tel (0 61 51) 94 56-0 • Fax (0 61 51) 94 56 80
