UNIVERSELLE PROZESSPLANUNG
3.Mai 2021-3.Mai 2021
URL: oksimo.org
Email: info@oksimo.org
Autor: Gerd Doeben-Henisch, gerd@oksimo.org
KONTEXT
Dieser Text ist Teil des Themas UNIVERSELLE PROZESSE PLANEN – Wie geht das? im oksimo.org Blog.
UNIVERSELLE PROZESSE PLANEN – Der Simulator Kern
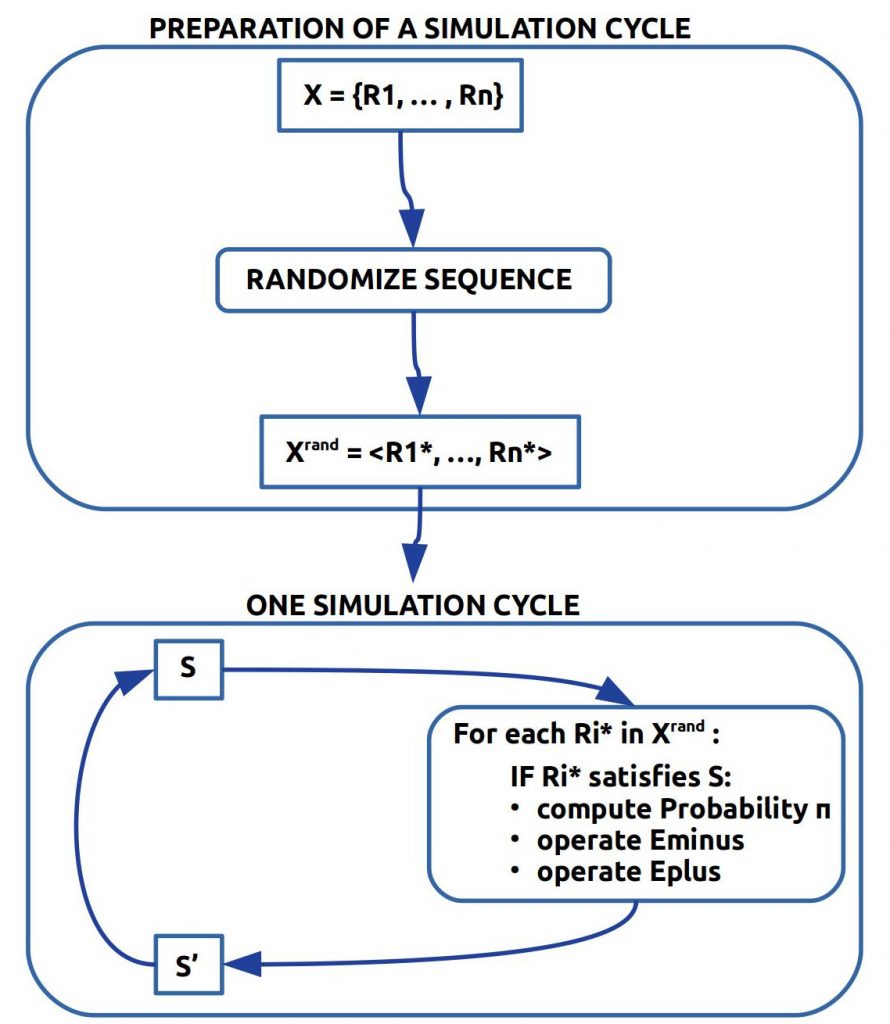
Für die konkrete Erstellung von oksimo Geschichten ist es vielfach wichtig, eine klare Vorstellung zu haben, wie der Simulator ‚im Kern‘ funktioniert, da der Simulator letztlich festlegt, auf welche Weise aus einer gegebenen Situation S mit gegebenen Veränderungsregeln X = {R1, …, Rn} ein neuer Nachfolgezustand S‘ entsteht: S |–Σ,X S‘
Für jeden Simulator-Zyklus (auch ‚Runde‘, ‚round‘ genannt), werden die verfügbaren Veränderungsregeln X (oder einfach nur ‚Regeln‘) in eine Zufallsreihenfolge Xrand gebracht. Diese Zufallsreihenfolge wird sequentiell abgearbeitet. Regeln, die in der realen Welt gleichzeitig/ parallel angewendet werden können, werden hier also in eine zufällige Abarbeitungsreihenfolge gebracht und dann nacheinander abgearbeitet.
Wenn S die Ausgangssituation ist, dann erzeugt der Simulator mit S |–Σ,Ri*S‘ eine Nachfolgesituation S‘, und wenn es noch weitere Regeln Rj* gibt, die angewendet werden können, dann wird S‘ zum neuen Ausgangspunkt für S“:
S1 |–Σ,Rj*S2, usw.
Anders geschrieben, der Ausdruck
ΣXrand(S)=S‘
ist nur eine Kurzschreibweise für einen Prozess, in dem der Simulator endliche viele Regeln Ri* aus Xrand auf S und die sich daraus ergebenden Nachfolgesituationen anwendet.
Anwendungsbeispiel
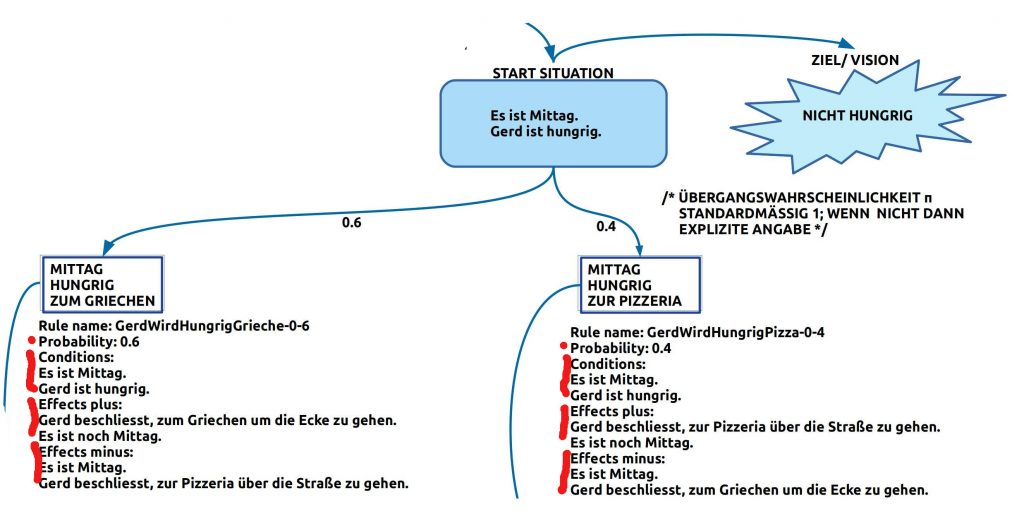
Hier ein kleines Beispiel, durch das verdeutlicht werden kann, was diese spezielle Arbeitsweise des Simulators bedeutet.
In diesem Beispiel gibt es eine Person ‚Gerd‘ die mittags hungrig ist (soll nicht ungewöhnlich sein :-)) und die zwischen zwei Möglichkeiten entscheiden kann: ‚Zum Griechen um die Ecke‘ oder ‚Zur Pizzeria über die Straße‘. Da der Grieche näher ist (und der Mensch tendenziell ‚bequem‘) ist die Wahrscheinlichkeit, zum Griechen um die Ecke zu gehen, eher 0.6 (60%), und die zur Pizzeria über die Straße etwa 0.4 (40%).
Im Simulator würden beide Regeln als ‚erfüllbar‘ klassifiziert und würden daher — mit unterschiedlicher Wahrscheinlichkeit — zur Anwendung gebracht. Die Reihenfolge ist mal so mal so: mal würde zuerst die Regel ‚Zum Griechen um die Ecke‘ angewendet, beim anderen Mal ‚Zur Pizzeria über die Straße‘. Wie auch immer, beide kämen zur Ausführung, falls die Wahrscheinlichkeit dies zulässt. Und bei p=0.6 bzw p=0.4, p’=0.6 x 0.4 = 0.24, kann es passieren.
Eine gleichzeitige Ausführung wäre im alltäglichen Leben aber ein bisschen ’schräg‘: eine Person X geht sowohl zum Griechen wie zur Pizzeria. Wer eine solche Simulation ‚lustig‘ findet, kann solch einen Ablauf sogar zulassen. Will man sich am gewohnten Alltag orientieren, dann müsste man verhindern, dass beide gleichzeitig zur Ausführung kommen können. Dies kann man dadurch erreichen,dass alle von der Parallelität betroffenen Regeln sich gegenseitig neutralisieren. Dies kann man dadurch erreichen, dass jede Regel die Eplus-Wirkungen der anderen Regeln explizit mit Eminus wieder löscht. Wenn also n-viele Regeln betroffenen wären und die Regel Ri* wäre die letzte, dann würde diese die Ri*-Eplus-Wirkungen aller anderen Regeln löschen, nur ihre eigenen Ri*-Eplus-Wirkungen würden erhalten bleiben. Diese Ri*-Eplus-Wirkungen wären dann der Anknüpfungspunkt für eine exklusive Fortsetzung.
