OKSIMO – UNIVERSELLE PROZESS PLANUNG
Veröffentlicht: 8.Sept. 2021 – 9.Sept. 2021
Email: info@oksimo.org
Autor: Gerd Doeben-Henisch (gerd@oksimo.org)
KONTEXT
Dieser Text ist Teil des Themenfeldes Oksimo und Theoriebildung des oksimo.org Blogs. In diesem Post wird das Thema anhand eines einfachen Beispiels illustriert.
OKSIMO und THEORIEBILDUNG – Vorbemerkung
Wie in einem anderen Post schon dargelegt wurde, entspricht jede Simulation in oksimo einer vollständigen Theorie, allerdings mit interessanten Besonderheiten.
Das Hauptproblem des Themas ‚wissenschaftliche empirische Theorie‚ besteht darin, dass es hierzu sehr viele Stimmen gibt, aber bis heute gibt es dennoch nicht die eine klare, von allen akzeptierte Auffassung, was eine wissenschaftliche Theorie ist. Eine kleine Auswahl von Büchern aus dem Themenspektrum findet sich hier: [1]- [5], [6] – [8], [9] – [12a,b], [14], [15]. Ein wichtiges Teilthema des übergreifenden Themas ‚wissenschaftliche empirische Theorie‘ ist das Thema ‚Logik‚. Das Thema Logik umfasst eine Geschichte von mehr als 2500 Jahren. Entsprechend umfangreich ist die Literatur. [16] ist eine — von vielen — Darstellungen zur Geschichte und [17] – [19] sind drei von sehr vielen Darstellungen zu den neueren Kernkonzepten von Aussagen- und Prädikatenlogik. Durch die modernen metatheoretischen Entwicklungen zum Folgerungsbegriff gibt es mittlerweile im Prinzip nahezu unendliche viele Logiken, von denen aber nur wenige wirklich im Gebrauch sind.
Als Wissenschaftsphilosoph und Forscher in einer Person muss man sich daher in dieser Vielfalt seine eigene Meinung bilden, die sich im Alltag bewähren muss.
Im Denkansatz, der diesem Post zugrunde liegt, gehen daher sehr viele Strömungen ein, die eine klare Zuordnung zu einem bestimmten Ansatz nicht erlauben.
Was in diesem Post — hoffentlich — deutlich werden wird, ist dass das oksimo Paradigma einerseits mit dem Standardkonzept von Logik radikal bricht, dass aber dann doch — durch die ‚Hintertür‘ der ’normalen Sprache‘ und der alltäglichen sprachlichen Bedeutung — die Grundkonzepte der Logik dennoch verfügbar sind. Eine vollständige Erfassung der ‚oksimo Logik‘ ist aber noch nicht geleistet. Aktuell sieht es so aus, als ob nicht nur alles möglich ist, was in den bekannten Konzepten möglich ist, sondern noch erheblich mehr.
Einfache empirische Theorie – Grundannahmen
Trotz der Vielfalt der Anschauungen zu dem, was eine empirische Theorie ist, gibt es einige Kernkonzepte, die die meisten Anschauungen teilen, wenngleich unterschiedlich in den Details und Gewichtungen, da die Voraussetzungen unterschiedlich sind.
In diesem Post werden die Kernkonzepte im Kontext der vorausgesetzten Annahmen angegeben, in der Hoffnung, dass dadurch der ganze begriffliche Rahmen transparenter wird.
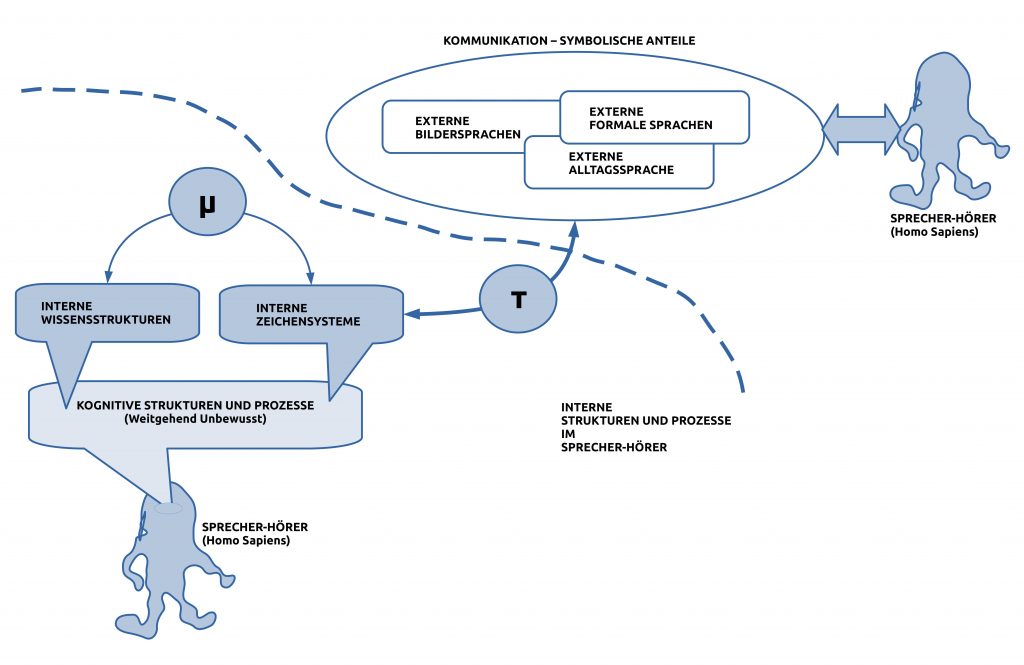
Von den vielfältigen Erscheinungsweisen zwischenmenschlicher Kommunikation werden hier nur drei Arten berücksichtigt, die im Kontext durchgängig vorkommen: externe Bildersprachen (Diagramme, Zeichnungen, Fotos, Videos, …), externe normale Sprachen sowie externe formale Sprachen. Von diesen drei Formen wird die normale Sprache als Normalfall angesehen und die beiden anderen Formen als Erweiterungen.
Externe Ausdrücke einer Sprache — egal ob Bild, normal oder formal — sind für sich genommen ohne jede Bedeutung. Erst durch eine aktive Korrespondenz zwischen externen Ereignissen und internen Symbolstrukturen können die externen Ausdrücke mit unterschiedlichen internen Wissensstrukturen und Wissensprozessen in Beziehung gesetzt werden. Ob dies tatsächlich geschieht und wie , dies hängt davon ab, (i) ob der betreffende Sprecher-Hörer die zugehörige Sprache gelernt hat, und wie er sie gelernt hat, und (ii) in welchem Kontext sich der Sprecher-Hörer gerade befindet. Dazu gehört fundamental eine Bedeutungsbeziehung μ, durch die eine Zuordnung zwischen Wissenselementen [C] und symbolischen Elementen [S] vorgenommen werden kann.[*] Mit S ⊆ C soll dann gelten: μ : S <—> C .
Ferner ist davon auszugehen, dass interne Strukturen und Prozesse überwiegend (mehr als 99%) unbewusst sind.
Einfache empirische Theorie – Intern und Extern
Nach diesen Vorüberlegungen ist vielleicht nachvollziehbar, dass die drei ‚Erscheinungsweisen‘ (Normalsprache, Bildsprache, Formale Sprache) wissenschaftlicher Rede grundsätzlich nur funktionieren können, wenn alle Beteiligten die jeweiligen Ausdrucksmengen durch gelernte Bedeutungsbeziehungen [μ] und gelernte Zuordnungsbeziehungen [τ] in hinreichend gleicher Weise verwenden. Und bei diesen zu unterstellenden Lernprozessen wird durchgehend gefordert werden müssen — wenn es um Fachsprachen im engeren Sinne gehen soll — dass die Verwendungssituationen, in denen die Bedeutung grundlegende trainiert wird, weitgehend standardisiert sind. Dies impliziert typische Kontexte. Neben diesen äußeren Strukturmerkmalen müssen aber auch die internen kognitiven Prozesse verfügbar und aktiv sein. Andernfalls bleiben die äußeren Merkmale einer Kommunikation bedeutungslos.
Empirische Beschreibungen
Sind alle die geforderten Bedingungen erfüllt, dann kann eine Gruppe von Experten [**] damit beginnen, sinnliche Wahrnehmungen einer gemeinsam geteilten beobachtbaren Welt als kognitive Gegebenheiten zu strukturieren, zu benennen, in Form von Beziehungsnetzen und Gesetzmäßigkeiten zu organisieren.
………
Eine empirische Theorie ist ein Text, der über einen bestimmten Ausschnitt der realen (beobachtbaren) Welt — dem Phänomenbereich — spricht. Dazu benötigt man unterschiedliche Mengen von Elementen, die in der Theorie behandelt werden sollen; eine minimale Menge von Relationen (Beziehungen) zwischen diesen Elementen; eine minimale Menge Axiomen; und letztendlich — wenngleich oft nicht explizit genannt — einen Folgerungsbegriff, der festlegt, wie man aus einer gegebenen Menge von wahren Aussagen wieder wahre Aussagen folgern/ ableiten kann. Diese gefolgerten wahren Aussage nennt man meistens Theoreme.
Im Folgenden wird das Beispiel einer ganz einfachen Theorie vorgestellt.
Als Phänomenbereich werden bestimmte Lebewesen untersucht, für die die Eigenschaften (1-stellige Relationen) ‚IstEinVogel()‚ und ‚KannFliegen()‚ vereinbart (durch Hinweis auf konkrete Beispiele). Die Zuordnung von Begriffen zu einer beobachtbaren Realität wird auch operationalisieren genannt: alle Beteiligten wissen dann, welche Form von beobachtbarer Realität mit den Ausdrücken gemeint ist.
Den beobachtbaren Objekten des Phänomenbereichs kann man auch eindeutige Namen zuordnen, z.B. durch Anbringen einer ‚Marḱierung‘ wie ‚N1′, “N223‘ usw. Alle mit Namen identifizierten Objekte bilden dann die endliche Menge der empirischen Objekte des Phänomenbereichs V_emp = {N1, N2, …, N223, …}.
Es wird hier angenommen, dass die Forscher für alle ihre benannten Objekte aus V_emp feststellen, dass bei ihnen die Eigenschaften ‚IstEinVogel()‚ und ‚KannFliegen()‚ durchgängig korrelieren, d.h. für jedes Objekt des Phänomenbereichs, für das gilt, dass es die eigenschaft hat, ein Vogel zu sein, gilt auch die Eigenschaft, dass es auch fliegen kann. Entsprechend der klassischen Logik könnte man dann Aussagen formulieren wie:
Wenn IstEinVogel(N1), dann KannFliegen(N1)
Aufgrund dieser Sachlage wird eine Arbeitshypothese gebildet der Art:
(A:x in V_emp)(Wenn IstEinVogel(x), dann KannFliegen(x))
In dieser Formel werden die konkreten Namen ersetzt durch eine Variable ‚x‘, die durch jeden konkreten Namen aus V_emp ersetzt werden kann, es gilt also: x ∈ V_emp
Wenn die Forscher mutig sind, dann wagen sie die Annahme, dass der bekannte Phänomenbereich V_emp nur ein Ausschnitt aus einem noch größeren Bereich ist, es also gilt:
V_emp ⊆ V
wobei die Elemente in V, die nicht in V_emp sind bislang noch nicht direkt beobachtet worden sind. Man nimmt aber an, dass es solche Objekte gibt und dass auf diese die beiden Eigenschaften IstEinVogel(x) und KannFliegen(x) zutreffen und dass auch für diese bislang noch nicht beobachteten Objekte der allgemeine Grundsatz gilt:
(A:x in V_emp)(Wenn IstEinVogel(x), dann KannFliegen(x))
Angenommen, man sieht eines Tages ein bislang noch nicht beobachtetes Objekt Nneu, auf das die Eigenschaft IstEinVogel(Nneu) zutrifft, und man erweitert die Menge V_emp um dieses neue Objekt, dann könnte man aus dem allgemeinen Grundsatz mittels der Ersetzungstabelle x ∈ V_emp die Aussage ableiten:
(x/Nneu) Wenn IstEinVogel(Nneu), dann KannFliegen(Nneu)
Da ja das Objekt mit Namen ‚Nneu‘ beobachtet wurde gilt die Aussage IstEinVogel(Nneu) als ‚wahr‘. Da mit folgt die andere Aussage KannFliegen(Nneu) auch als wahre Aussage.
Sofern man dann irgendwann beobachten kann, dass das als ‚Vogel‘ klassifizierte Objekt Nneu tatsächlich fliegen kann, ist der allgemeine Grundsatz für das neue Objekt bestätigt. Kommt man nach einiger Zeit aber zum gegenteiligen Eindruck, dass die Behauptung, dass Nneu fliegen könne, falsch sei, dann lässt sich die Behauptung nicht bestätigen; möglicherweise klassifiziert man das Objekt sogar als ¬KannFliegen(Nneu). Rein formal hat man dann einen logischen Widerspruch der Art
¬KannFliegen(Nneu) & KannFliegen(Nneu)
Damit wäre dann die allgemeine Annahme, dass alle Objekte aus dem Phänomenbereich V_emp, die die Eigenschaft haben, ein Vogel zu sein, auch fliegen können, widerlegt.
In der Realität gibt es ja Beispiele von Vögel (z.B. Vogel Strauß), die nicht fliegen können.
Die Methode, den empirischen Phänomenbereich V_emp nur über explizite Markierungen zu definieren, ist allerdings sehr aufwendig (wenngleich zuverlässig). Tatsächlich ist solch eine explizite Benennung ja nur möglich, weil alle beteiligten Forscher sich darauf einigen können, dass eine zuvor operationalisierte Eigenschaft IstEinVogel() erkennbar und entscheidbar ist. Denkbar wäre z.B. als Klassifikationskriterium dafür, dass man von einem Objekt sagt, dass es ein Vogel ist, wenn dieses Objekt zwei Flügel besitzt (HatZweiFlügel()). Dann könnte man einfacher sagen:
- Es gibt ein Objekt a, das zwei Flügel hat
- HatZweiFlügel(a)
- Ein Objekt, das zwei Flügel hat, ist ein Vogel
- (A:x)(Wenn HatZweiFlügel(x), dann IstEinVogel(x))
- Wenn HatZweiFlügel(a), dann IstEinVogel(a)
- IstEinVogel(a)
Dann könnte man für beliebige Objekte, für die man entscheiden kann, dass sie zwei Flügel haben, folgern, dass sie ein Vogel sind.
Einfache empirische Theorie mit oksimo
Nehmen wir nochmals das einfache Beispiel vom vorausgehenden Abschnitt:
<V, IstEinVogel(), KannFliegen(), „Alle Vögel können fliegen“, ⊩>
Die Frage stellt sich, wie man dieses mittels oksimo realisieren kann.
Klar ist, dass man in oksimo mit folgender Grundstruktur arbeitet:
< Ausgangslage [S0], Ziel [V0], Regeln [R], Simulator [Σ]>
Wir wissen, dass in oksimo der Simulator ∑ Veränderungsregeln R auf eine gegebene Situation S so anwenden kann, dass daraus eine Nachfolge-Situation S‘ gefolgert werden kann. Veränderungsregeln in oksimo haben das Format WENN C, DANN Änderung, genauer:
WENN Bedingung C erfüllt, DANN soll Eplus und Eminus gelten.
Dies kann bedeuten:
WENN Hans ist ein Vogel, DANN Hans kann fliegen
D.h. wenn in einem aktuellen Zustand S der Ausdruck ‚Hans ist ein Vogel‘ vorkommt, dann kann der Ausdruck ‚Hans kann fliegen‘ zu S hinzugefügt werden , also
S ={Hans ist ein Vogel}
S‘ = {Hans ist ein Vogel, Hans kann fliegen}
In dem vorausgehenden Beispiel einer einfachen klassischen empirischen Theorie wird mit Variablen gearbeitet, als z.B. ‚x‘. Diese Variablen stehen für alle möglichen Elemente der allgemeinen Menge V. Sofern definiert, kann man die Variablen durch Konstanten ersetzen, wie im Beispiel durch die Menge der Konstanten V_emp := {Hans, Peter, Emil, N2, M34, …}
Es stellt sich die Frage, ob und wie man in oksimo mit Variablen und Konstanten umgehen kann.
Regel R1: Wenn ‚X ist ein Vogel‘, dann ‚Hans ist ein Vogel‘
Regel R2: WENN ‚Hans ist ein Vogel‘, DANN ‚Hans kann fliegen‘
S ={X ist ein Vogel}
Mit R1:
S‘ ={X ist ein Vogel, Hans ist ein Vogel}
Mit R2:
S“ = {X ist ein Vogel, Hans ist ein Vogel, Hans kann fliegen}
Erweiterungen in oksimo:
Wenn ich eine Ersetzungsanweisung habe der Art:
X = {Hans, Peter, Emil, N2, M34}
Dann könnte ein Ausdruck wie
S ={X ist ein Vogel}
übersetzt werden in einen Ausdruck, wo das ‚X‘ durch ein Element aus der Ersetzungstabelle ersetzt wurde, also z.B.:
S‘ ={Hans ist ein Vogel, Peter ist ein Vogel, … }
ANMERKUNGEN
[*] Da interne symbolische Elemente letztlich auch Wissenselemente sind, können interne symbolische Elemente auch ‚mit sich selbst‘ korrelieren.
[**] In diesem Text wird angenommen, dass jeder Mensch ein Experte ist.
[1] Philosophy of Science, Wikipedia [EN]: https://en.wikipedia.org/wiki/Philosophy_of_science (9.Sept.2021)
[2] Lohse, Simon und Reydon, Thomas (Hg) (2017), Grundriss Wissenschaftsphilosophie. Die Philosophien der ‚Einzelwissenschaften.Felix Meiner Verlag, Hamburg.
[3] Jürgen Mittelstraß (Ed.), Enzylopädie Philosophie und Wissenschaftstheorie, Bd.1-4, Publisher J.Metzler, Stuttgart – Weimar (Germany), 1995 – 1996
[4] Hans Jörg Sandkühler (Ed.), Enzylopädie Philosophie, Bd. 1-3, Publisher Felix Meiner Verlag, Hamburg (Germany), 2010. Stichworte ‘Wissenschaftsphilosophie‘ und ‘Wissenschaftstheorie‘ in Bd.3
[5] F. Suppe, editor. The Structure of Scientific Theories. University of
Illinois Press, Urbana, 2 edition, 1979.
[6] John Dewey, Logic. The Theory Of Inquiry, New York, Henry Holt and Company, 1938 (see: https://archive.org/details/JohnDeweyLogicTheTheoryOfInquiry with several formats; I am using the kindle (= mobi) format: https://archive.org/download/JohnDeweyLogicTheTheoryOfInquiry/%5BJohn_Dewey%5D_Logic_-_The_Theory_of_Inquiry.mobi . This is for the direct work with a text very convenient. Additionally I am using a free reader ‘foliate’ under ubuntu 20.04: https://github.com/johnfactotum/foliate/releases/). The page numbers in the text of the review — like (p.13) — are the page numbers of the ebook as indicated in the ebook-reader foliate.(There exists no kindle-version for linux (although amazon couldn’t work without linux servers!))
[7] Karl Popper, The Logic of Scientific Discovery, First published 1935 in German as Logik der Forschung, then 1959 in English by Basic Books, New York (more editions have been published later; I am using the eBook version of Routledge (2002))
[8] Jules Henri Poincaré (1854 – 1912),https://en.wikipedia.org/wiki/Henri_Poincar%C3%A9, La science et l’hypothèse, Paris 1902, English: Science and Hypothesis, New York 1905, publisher The Walter Scott Publishing CO., LTD (See wikisource: https://en.wikisource.org/wiki/Science_and_Hypothesis )
[9] Balzer, Wolfgang und Moulines, C.Ulises und Sneed, Joseph D. (Hg), (1987), AN ARCHITECTONIC FOR SCIENCE. The Sturcturalist Program. D.Reidel Publishing Company, Dordrecht et.al.
[10] Balzer, Wolfgang (1982), Empirische Theorien: Modelle, Strukturen, Beispiele. Friedrich Viehweg & Sohn, Braunschweig – Wiesbaden
[11] Ludwig, G. (1978). Die Grundstrukturen einer physikalischen Theorie. Springer-Verlag, Berlin – Heidelberg – New York.
[12a] Bourbaki, N. (1970) ÉLÉMENTS DE MATHÉMATIQUE. Théorie des Ensembles. Verlag Hermann, Paris
[12b] Bourbaki, N. (1968) Theory od Sets. Hermann & Addison-Wesley, Paris
[13] Scheibe, Erhard (1997) Die Reduktion physikalischer Theorien. Ein Beitrag zur Einheit der Physik. Springer-VerlagBerlin Heidelberg GmbH
[14] Thomas S.Kuhn (1962), „The Structure of Scientific Revolution“, University of Chicago Press
[15] Kenneth Craik. The Nature of Explanation. Cambridge University Press, Cambridge (UK), 1 edition, 1943
[16] Kneale, William und Martha (1962, repr. mit Korrekturen 1986), The Development of Logic. Clraendon >Prsess, Oxford
[17] Hinst, Peter (1974), Logische Propädeutik. Wilhelm Fink Verlag, München
[18] Hilbert, D. und Ackermann, W. (1972, 6.Aufl.) Grundzüge der theoretischen Logik. Springer-Verlag, Berlin – Heidelberg – New York
[19] Quine, Willard van Orman (DE 1969m EN 1964), Grundzüge der Logik.Suhrkamp Verlag, Frankfurt am Main
